Question

Cho △ABC, Â = 90^o, AB = AC, M là trung điểm của BC, E là một điểm bất kì nằm giữa M và C. Kẻ BH ⊥ AE, CK ⊥ AE (H, K trên đường thẳng AE). Chứng minh rằng:

a) BK = AK.

b) △MBH = △MAK.

c) △MHK vuông cân.

Có thể phải kẻ thêm nhưng đây là hình gốc nè:

Answer 1

- Không kẻ hình nữa nhé ~
Chứng minh :
a) \(\widehat{ABH}+\widehat{BAH}+\widehat{BHA}=180^o\left(\text{đ/l tổng 3 góc của 1 t/g}\right)\)
Mà \(\widehat{BHA}=90^o\left(gt\right)\)
\(\Rightarrow\widehat{ABH}+\widehat{BAH}=180^o-90^o\)
\(\Rightarrow\widehat{ABH}+\widehat{BAH}=90^o\)
Mà \(\widehat{BAH}+\widehat{HAC}=90^o\)
\(\Rightarrow\widehat{ABH}=\widehat{HAC}\)
Xét △BHA vuông tại H và △AKC vuông tại K có:
BA = AC ( gt )
\(\widehat{ABH}=\widehat{HAC}\left(cmt\right)\)
⇒△BHA = △AKC ( ch - gn )
⇒ BH = AK ( tương ứng )
b) Nối A -> M ; K -> M
Xét △BMA và △CMA có:
BA = CA ( gt )
AM - cạnh chung
BM = CM ( gt )
⇒ △BMA = △CMA ( c.c.c )
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\left(\text{tương ứng}\right)\)
\(\Rightarrow\widehat{BMA}=\widehat{AMC}\left(\text{tương ứng}\right)\)
Mà \(\widehat{BMA}+\widehat{AMC}=180^o\left(\text{kề bù}\right)\)
\(\Rightarrow\widehat{BMA}=\widehat{AMC}=90^o\)
Có M là trung điểm của BC
⇒ Tia AM nằm giữa AB và AC
\(\Rightarrow\widehat{BAM}+\widehat{MAC}=\widehat{BAC}\)
\(\Rightarrow\widehat{BAM}+\widehat{MAC}=90^o\)
Mà \(\widehat{BAM}=\widehat{MAC}\left(cmt\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{MAC}=45^o\)
Có \(\widehat{BAM}+\widehat{AMB}+\widehat{ABM}=180^o\left(\text{đ/l tổng 3 góc của 1 t/g}\right)\)
\(\Rightarrow\widehat{ABM}=180^o-90^o-45^o\)
\(\Rightarrow\widehat{ABM}=45^o\)
\(\Rightarrow\widehat{BAM}=\widehat{ABM}\left(=45^o\right)\)
⇒ △ABM cân tại M
⇒ MB = MA
Có E nằm giữa M và C
⇒ Tia AE nằm giữa AC và AM
\(\Rightarrow\widehat{CAH}+\widehat{HAM}=\widehat{MAC}=45^o\)
\(\Rightarrow\widehat{HAM}=45^o-\widehat{CAH}\)
Có \(\widehat{ABH}+\widehat{HBE}=45^o\)
\(\Rightarrow\widehat{HBE}=45^o-\widehat{ABH}\)
Mà \(\widehat{CAH}=\widehat{ABH}\left(cmt\right)\Rightarrow\widehat{HAM}=\widehat{HBE}\)
Xét △MBH và △MAK có :
BM = MA ( cmt )
\(\widehat{HAM}=\widehat{HBE}\left(cmt\right)\)
BH = AK ( cmt )
⇒ △MBH = △MAK ( c.g.c )
⇒ MH = MK ( tương ứng ) (1)
\(\Rightarrow\widehat{BMH}=\widehat{AMK}\left(\text{tương ứng}\right)\)
c)
Có\(\widehat{AMB}+\widehat{AMH}=\widehat{BMH}\)
\(\Rightarrow\widehat{AMH}=\widehat{BMH}-90^o\)
Có \(\widehat{AMC}+\widehat{CMK}=\widehat{AMK}\)
\(\Rightarrow\widehat{CMK}=\widehat{AMK}-90^o\)
Mà\(\widehat{BMH}=\widehat{AMK}\left(cmt\right)\)
\(\Rightarrow\widehat{AMH}=\widehat{CMK}\)
Mà\(\widehat{AMH}+\widehat{HMC}=90^o\)
\(\Rightarrow\widehat{CMK}+\widehat{HMC}=90^o\)
\(\Rightarrow\widehat{HMK}=90^o\)(2)
Từ (1) và (2) ⇒ △HMK vuông cân

Answer 2

Nguyễn Thanh HằngVõ Đông Anh Tuấnnguyen thi vangAkai HarumaNguyễn Thị Bích Thủy๖ۣۜĐặng♥๖ۣۜQuýTNA AtulaRibi Nkok NgokVương Đại NguyênGia Hân NgôĐẹp Trai Không Bao Giờ SaiJingle BellLightning FarronLê BùiVũ ElsaNguyễn Huy Túsoyeon_Tiểubàng giảiTrần Việt LinhHoàng Lê Bảo Ngọc

Answer 3

Đây là Bài Toán nằm trong kỳ thi SAT năm 1982 và chỉ có 3 trong số 300.000 thí sinh đưa ra câu trả lời chính xác.

SAT là một kỳ thi phổ biến nhằm sát hạch học sinh, sinh viên trong các kỳ thi tuyển sinh vào hệ đại học cao đẳng tại Mỹ.

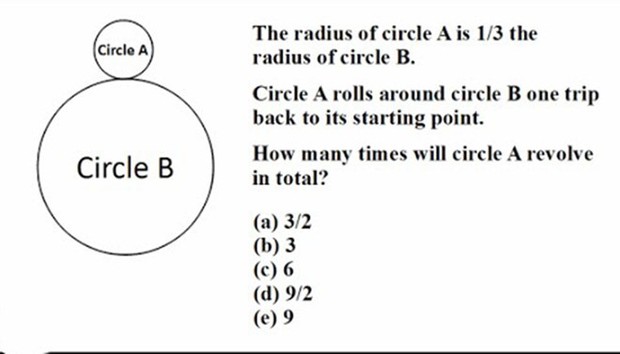
Đề bài như sau: Bán kính hình tròn B gấp 3 lần bán kính hình tròn A. Nếu hình A lăn xung quanh hình B, nó phải thực hiện bao nhiêu vòng quay để trở lại điểm xuất phát?

Các phương án được đưa ra là 3/2, 3, 6, 9/2, 9 vòng.

 

Rất nhiều người và cả phần lớn thí sinh dự kỳ thi SAT năm đó đều chọn phương án B là phương án trả lời đúng.

Nếu lấy hệ quy chiếu là vòng tròn A, nó chỉ tự quay quanh 3 vòng. Nhưng nếu hệ quy chiếu không nằm trên vòng A, nó đã quay được 4 vòng, vòng thứ tư là do vòng tròn B tặng thêm.

Ngày 25/5/1982, tờ Washington Post đã đăng tải 1 bài viết cho rằng cả 5 phương án trên đều sai.

Theo lập luận của tác giả bài viết, câu hỏi nhắc đến "revolve" nghĩa là hình tròn A vừa tự xoay quanh nó vì xoay quanh hình tròn B. Đáp án thực sự của bài toán là 4