a: Xét tứ giác DHKC có \(\hat{DHC}=\hat{DKC}=90^0\)
nên DHKC là tứ giác nội tiếp
b: Xét (O) có
\(\hat{ABD};\hat{ACD}\) là các góc nội tiếp chắn cung AD
Do đó: \(\hat{ABD}=\hat{ACD}\)
=>\(\hat{ACD}=60^0\)
Xét (O) có
ΔCDA nội tiếp
CA là đường kính
Do đó: ΔCDA vuông tại D
Xét ΔCDA vuông tại D có \(cosC=\frac{CD}{CA}\)
=>\(\frac{CD}{4}=cos60=\frac12\)
=>CD=2(cm)
Diện tích tam giác CDA là:
\(S_{CDA}=\frac12\cdot CD\cdot CA\cdot\sin DCA\)
\(=\frac12\cdot2\cdot4\cdot\sin60=4\cdot\sin60=4\cdot\frac{\sqrt3}{2}=2\sqrt3\left(\operatorname{cm}^2\right)\)













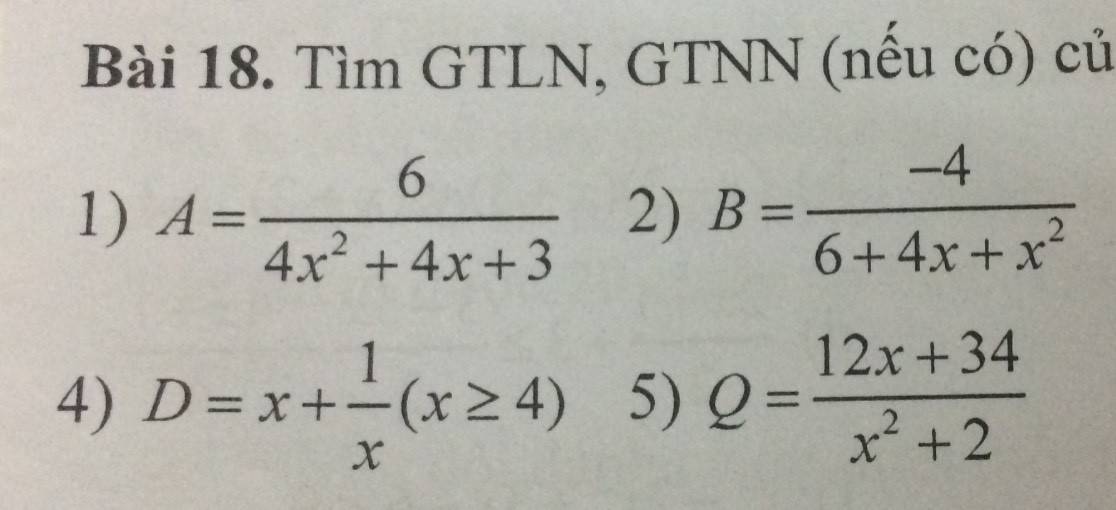

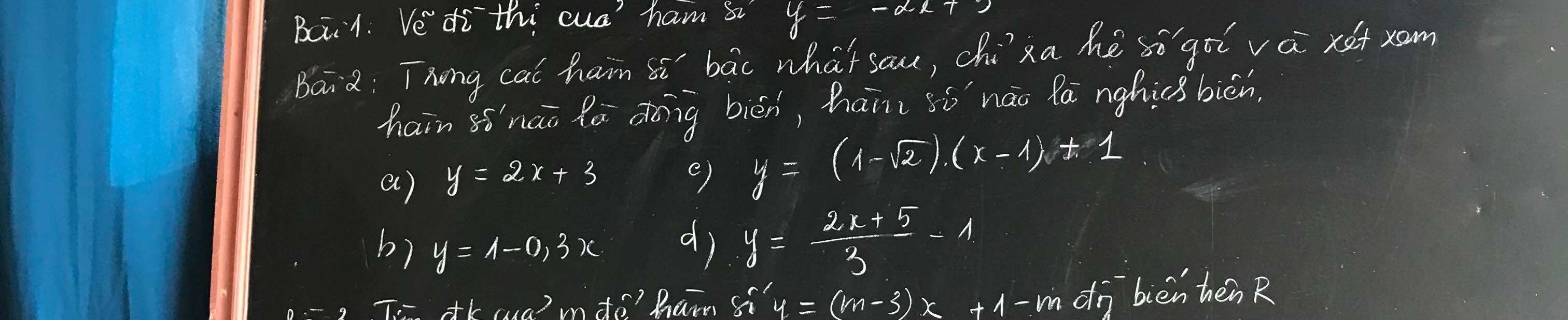

 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ






