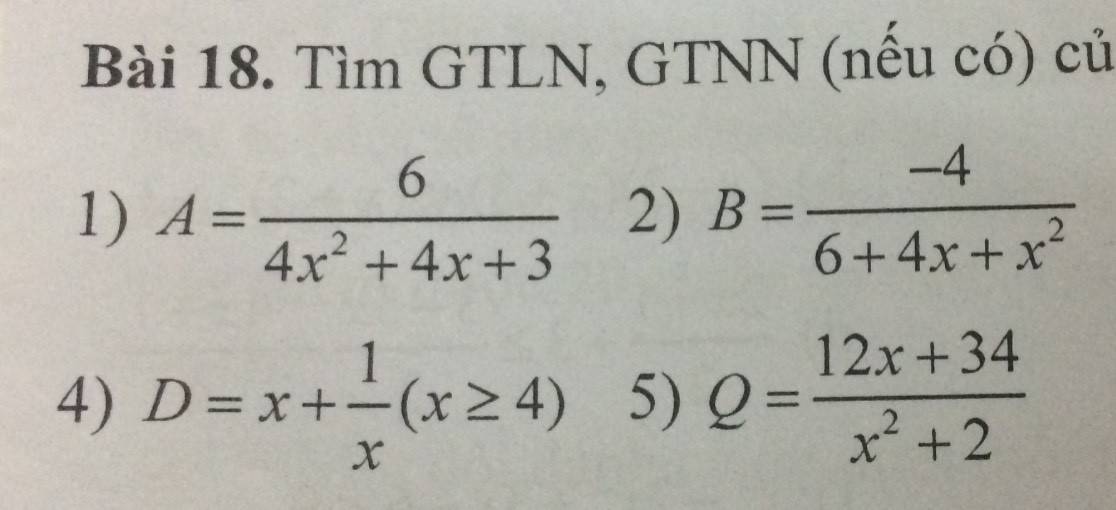1.
Ta có: $4x^2+4x+3=(4x^2+4x+1)+2=(2x+1)^2+2\geq 0+2=2$
$\Rightarrow A=\frac{6}{4x^2+4x+3}\leq \frac{6}{2}=3$
Vậy $A_{\max}=3$. Giá trị này đạt tại $2x+1=0\Leftrightarrow x=\frac{-1}{2}$
2.
$6+4x+x^2=(x^2+4x+4)+2=(x+2)^2+2\geq 0+2=2$
$\Rightarrow \frac{4}{6+4x+x^2}\leq \frac{4}{2}=2$
$\Rightarrow \frac{-4}{6+4x+x^2}\geq -2$
$\Rightarrow B\geq -2$
Vậy $B_{\min}=-2$. Giá trị này đạt tại $x+2=0\Leftrightarrow x=-2$
4.
$D=x+\frac{1}{x}=\frac{15x}{16}+(\frac{x}{16}+\frac{1}{x})$
Do $x\geq 4$ nên $\frac{15x}{16}\geq \frac{15.4}{16}=\frac{15}{4}$
$\frac{x}{16}+\frac{1}{x}\geq 2\sqrt{\frac{1}{16}}=\frac{1}{2}$
$\Rightarrow D=\frac{15x}{16}+(\frac{x}{16}+\frac{1}{x})\geq \frac{15}{4}+\frac{1}{2}=\frac{17}{4}$
Vậy $D_{\min}=\frac{17}{4}$. Giá trị này đạt được khi $x=4$
5.
Áp dụng BĐT Cô-si:
$x^2+\frac{1}{9}\geq 2\sqrt{\frac{x^2}{9}}=\frac{2x}{3}$
$\Rightarrow x^2+2=(x^2+\frac{1}{9})+\frac{17}{9}\geq \frac{2x}{3}+\frac{17}{9}=\frac{6x+17}{9}$
$\Rightarrow \frac{12x+34}{x^2+2}\leq \frac{12x+34}{\frac{6x+17}{9}}=\frac{9(12x+34)}{6x+17}=\frac{18(6x+17)}{6x+17}=18$
Vậy $Q_{\max}=18$. Giá trị này đạt tại $x=\frac{1}{3}$