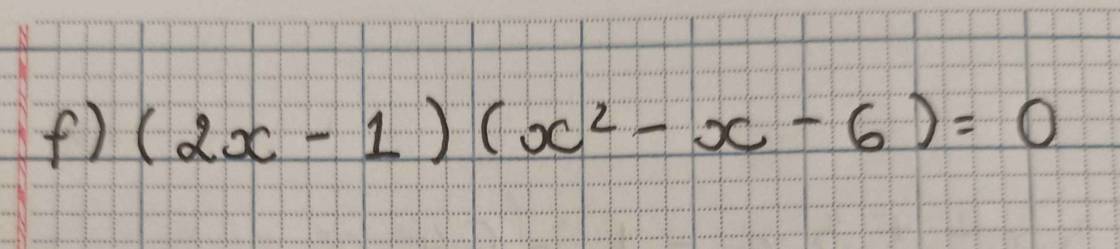\(\left(2x-1\right)\left(x^2-x-6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-1=0\\x^2-x-6=0\left(1\right)\end{matrix}\right.\)
Giải pt `(1)` ta có
`x^2-x-6=0`
\(\Delta=\left(-1\right)^2-4.\left(-6\right)=25>0\\ \Rightarrow\sqrt{\Delta}=5\)
pt có `2` nghiệm pb
\(x_1=\dfrac{1+5}{2}=3\\ x_2=\dfrac{1-5}{2}=-2\)
Vậy ta có
\(\left[{}\begin{matrix}2x=1\\x=3\\x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=3\\x=-2\end{matrix}\right.\)
\(\left(2x-1\right)\left(x^2-x-6\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2+2x-3x-6\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left[x\left(x+2\right)-3\left(x+2\right)\right]=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x+2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\x+2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-2\\x=3\end{matrix}\right.\)
$\text{#}Toru$