Đặt \(A=4x^3+14x^2+9x-6\)
\(\Leftrightarrow A=\left(x+2\right)\left(4x^2+6x-3\right)\)
Để A là số chính phương thì \(x+2=4x^2+6x-3\) (1) hoặc \(x+2\) và \(4x^2+6x-3\) có dạng chính phương (2)
Giải trường hợp (1) \(\Rightarrow4x^2+5x-5=0\)
\(\Delta=5^2+4\cdot4\cdot5=105>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-5+\sqrt{105}}{8}\\x=\dfrac{-5+\sqrt{105}}{8}\end{matrix}\right.\) (loại do cả 2 đều âm KTM đề bài)
Giải trường hợp (2):
Đặt \(\left\{{}\begin{matrix}x+2=a^2\\4x^2+6x-3=b^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2=a^2\\4x\left(x+2\right)-2\left(x+2\right)+1=b^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=a^2-2\\4\left(a^2-2\right)a^2-2a^2+1=b^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=a^2-2\\4a^4-10a^2+1=b^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=a^2-2\\\left(2a^2-\dfrac{5}{2}\right)^2-\dfrac{21}{4}=b^2\left(3\right)\end{matrix}\right.\)
Giải (3), ta được:
\(\left(4a^2-5\right)^2-21=4b^2\)
\(\Leftrightarrow\left(4a^2-5\right)^2-4b^2=21\)
\(\Leftrightarrow\left(4a^2-5-2b\right)\left(4a^2-5+2b\right)=21\cdot1=1\cdot21=3\cdot7=7\cdot3\)
Với \(\left\{{}\begin{matrix}4a^2-5-2b=1\\4a^2-5+2b=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^2-5+2b=21\\b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^4-10a^2+1=25\\b=5\end{matrix}\right.\)
Đặt \(a^2=t\left(t>0\right)\)\(\Leftrightarrow4t^2-10t-24=0\Leftrightarrow\left[{}\begin{matrix}t=4\left(N\right)\\t=-\dfrac{3}{2}\left(L\right)\end{matrix}\right.\)
\(\Leftrightarrow a^2=4\Leftrightarrow x=2\left(N\right)\)
Với \(\left\{{}\begin{matrix}4a^2-5-2b=3\\4a^2-5+2b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^2-5+2b=7\\b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^4-10a^2+1=1\\b=1\end{matrix}\right.\)
\(\Leftrightarrow2a^2\left(2a^2-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a^2=0\\2a^2=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\left(L\right)\\x=\dfrac{5}{2}-2\left(L\right)\end{matrix}\right.\)
Tương tự với hai trường hợp còn lại ta cũng ra nghiệm giống như trên.
Vậy \(x=2\) thì A là số chính phương
Tick nha bạn 😘
đề này ôn học sinh giỏi toán hả bạn?
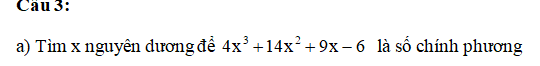
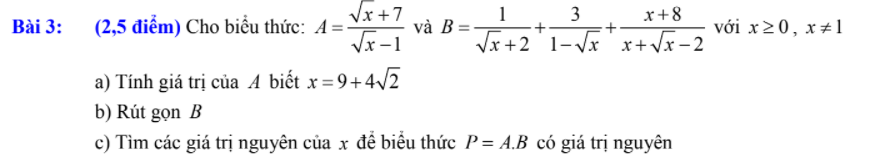được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 
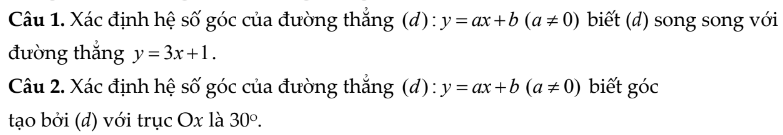
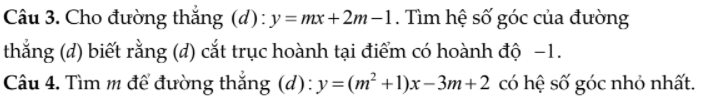này được 