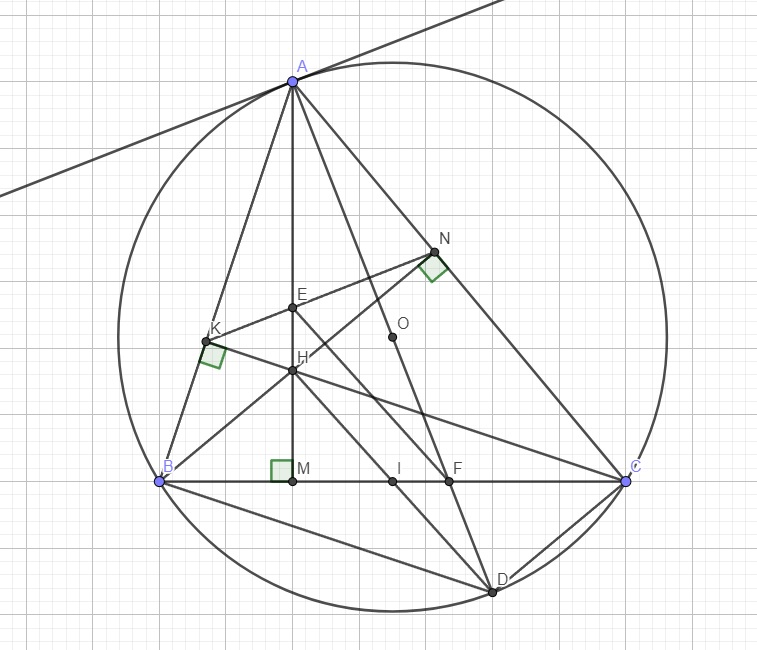
\(\widehat{ACD}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ACD}=90^0\)
Mà \(\widehat{ABC}=\widehat{ADC}\) (cùng chắn AC)
\(\Rightarrow\Delta_VAMB\sim\Delta_VACD\left(g.g\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{DAC}\) (1)
Do AKHN nội tiếp \(\Rightarrow\widehat{AKE}=\widehat{AHN}\) (cùng chắn AN)
\(\widehat{AHN}+\widehat{MHN}=180^0\) (kề bù)
M và N cùng nhìn CH dưới 1 góc vuông \(\Rightarrow MHNC\) nội tiếp
\(\Rightarrow\widehat{MHN}+\widehat{ACF}=180^0\)
\(\Rightarrow\widehat{AKE}=\widehat{ACF}\) (2)
(1);(2) \(\Rightarrow\Delta AKE\sim\Delta ACF\left(g.g\right)\)
\(\Rightarrow\dfrac{AK}{AC}=\dfrac{AE}{AF}\)
Lại có: \(\widehat{AKH}=\widehat{ACD}=90^0\) (3)
(1);(3) \(\Rightarrow\Delta AKH\sim\Delta ACD\left(g.g\right)\)
\(\Rightarrow\dfrac{AK}{AC}=\dfrac{AH}{AD}\)
\(\Rightarrow\dfrac{AE}{AF}=\dfrac{AH}{AD}\Rightarrow\dfrac{AE}{AH}=\dfrac{AF}{AD}\)
\(\Rightarrow EF||HD\) (4)
Do CD và BH cùng vuông góc AC (gt) \(\Rightarrow CD||BH\)
Tương tự, BD và CH cùng vuông góc AB \(\Rightarrow BD||CH\)
\(\Rightarrow BHCD\) là hình bình hành
\(\Rightarrow BC\) và HD cắt nhau tại trung điểm mỗi đường
I là trung điểm BC \(\Rightarrow I\) là trung điểm HD hay H, D, I thẳng hàng (5)
(4);(5) \(\Rightarrow EF||HI\)