Các câu hỏi tương tự
Biết đồ thị hàm số
y
x
-
2
x
+
1
các trục Ox,Oy lần lượt tại hai điểm phân biệt A, B. Tính diện tích S của tam giác OAB A. S1 B.
S
1
2
C.
S
2
D.
S
4
Đọc tiếp
Biết đồ thị hàm số y = x - 2 x + 1 các trục Ox,Oy lần lượt tại hai điểm phân biệt A, B. Tính diện tích S của tam giác OAB
A. S=1
B. S = 1 2
C. S = 2
D. S = 4
Cho hàm số
y
x
3
-
3
x
2
+
m
1
. Tìm m để tiếp tuyến của đồ thị (1) tại điểm có hoành độ bằng 1 cắt các trục Ox, Oy lần lượt tại các điểm A, B mà diện tích tam giác OAB bằng
3
2
A.
m
3
h
o
ặ
c
m
-...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + m 1 . Tìm m để tiếp tuyến của đồ thị (1) tại điểm có hoành độ bằng 1 cắt các trục Ox, Oy lần lượt tại các điểm A, B mà diện tích tam giác OAB bằng 3 2
A. m = 3 h o ặ c m = - 1
B. m = 2
C. m = - 4 h o ặ c m = 2
D. m = 3
Cho hàm số
y
x
3
−
3
x
2
+
m
(1). Tìm m để tiếp tuyến của đồ thị (1) tại điểm có hoành độ bằng 1 cắt các trục Ox, Oy lần lượt tại các điểm A, B mà diện tích tam giác OAB bằng
3
2
. A. m 2 B. m 3 hoặc m -1 C. m 4 hoặc m 2 D. m 3
Đọc tiếp
Cho hàm số y = x 3 − 3 x 2 + m (1). Tìm m để tiếp tuyến của đồ thị (1) tại điểm có hoành độ bằng 1 cắt các trục Ox, Oy lần lượt tại các điểm A, B mà diện tích tam giác OAB bằng 3 2 .
A. m = 2
B. m = 3 hoặc m = -1
C. m = 4 hoặc m = 2
D. m = 3
Cho đồ thị hàm số
C
:
y
1
x
;
điểm M có hoành độ
x
M
2
−
3
thuộc (C). Biết tiếp tuyến của (C) tại M lần lượt cắt Ox, Oy tại A, B. Tính diện tích tam giác OAB. A.
S
Δ
O
A
B
1.
B....
Đọc tiếp
Cho đồ thị hàm số C : y = 1 x ; điểm M có hoành độ x M = 2 − 3 thuộc (C). Biết tiếp tuyến của (C) tại M lần lượt cắt Ox, Oy tại A, B. Tính diện tích tam giác OAB.
A. S Δ O A B = 1.
B. S Δ O A B = 4.
C. S Δ O A B = 2.
D. S Δ O A B = 2 + 3 .
Cho hàm số
y
x
+
2
2
x
+
3
có đồ thị (C). Giả sử, đường thẳng d: ykx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. Tổng k+m có giá trị bằng: A. 1. B. 3. C. -1 D. -3
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Giả sử, đường thẳng d: y=kx+m là tiếp tuyến của (C), biết rằng d cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. Tổng k+m có giá trị bằng:
A. 1.
B. 3.
C. -1
D. -3
Cho đồ thị hàm số yf(x) đi qua gốc tọa độ O, ngoài ra còn cắt trục Ox tại các điểm có hoành độ lần lượt bằng ‒3 và 4 như hình bên. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số và trục Ox. A.
S
∫
−
3
4
f
x
d
x
B.
S
∫
−...
Đọc tiếp
Cho đồ thị hàm số y=f(x) đi qua gốc tọa độ O, ngoài ra còn cắt trục Ox tại các điểm có hoành độ lần lượt bằng ‒3 và 4 như hình bên. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số và trục Ox.
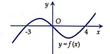
A. S = ∫ − 3 4 f x d x
B. S = ∫ − 3 0 f x d x + ∫ 0 4 f x d x
C. S = ∫ − 3 0 f x d x + ∫ 4 0 f x d x
D. S = ∫ 0 - 3 f x d x + ∫ 0 4 f x d x
Giả sử đồ thị (C) của hàm số
y
(
2
)
x
ln
2
cắt trục tung tại điểm A và tiếp tuyến của (C) tại A cắt trục hoành tại B. Tính diện tích S của tam giác AOB A.
S
1
ln
2
B.
S...
Đọc tiếp
Giả sử đồ thị (C) của hàm số y = ( 2 ) x ln 2 cắt trục tung tại điểm A và tiếp tuyến của (C) tại A cắt trục hoành tại B. Tính diện tích S của tam giác AOB
A. S = 1 ln 2
B. S = ( 1 ln 2 ) 2
C. S = ( 1 ln 2 ) 3
D. S = ( 1 ln 2 ) 4
Cho hàm số
y
x
+
2
2
x
+
3
H
.
Viết phương trình tiếp tuyến của đồ thị hàm số (H), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O. A.
y
-
x...
Đọc tiếp
Cho hàm số y = x + 2 2 x + 3 H . Viết phương trình tiếp tuyến của đồ thị hàm số (H), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O.
A. y = - x - 2 .
B. y = - x + 1 .
C. y = -x + 2
D. y = - x và y = -x-2
Giả sử đồ thị (C) của hàm số
y
2
x
ln
2
cắt trục tung tại điểm A và tiếp tuyến của (C) tại A cắt trục hoành tại B. Tính diện tích S của tam giác AOB. A.
S
1
ln
2
B.
S
1
ln...
Đọc tiếp
Giả sử đồ thị (C) của hàm số y = 2 x ln 2 cắt trục tung tại điểm A và tiếp tuyến của (C) tại A cắt trục hoành tại B. Tính diện tích S của tam giác AOB.
A. S = 1 ln 2
B. S = 1 ln 2 2
C. S = 1 ln 2 3
D. S = 1 ln 2 4




