\(x^{a^2-b^2}=x^{16}\Rightarrow a^2-b^2=16\)
\(\Rightarrow a-b=\dfrac{a^2-b^2}{a+b}=\dfrac{16}{2}=8\)
\(x^{a^2-b^2}=x^{16}\Rightarrow a^2-b^2=16\)
\(\Rightarrow a-b=\dfrac{a^2-b^2}{a+b}=\dfrac{16}{2}=8\)
Tính các nguyên hàm.
a)\(\int\dfrac{2dx}{x^2-5x}=A\ln\left|x\right|+B\ln\left|x-5\right|+C\) . Tìm 2A-3B.
b)\(\int\dfrac{x^3-1}{x+1}\)dx=\(Ax^3-Bx^2+x+E\ln\left|x+1\right|+C\).Tính A-B+E
Tìm x, biết ( 1 4 ) x = 16
A. x = -2 B. x = 2
C. x = 1/2 D. x = -1/2
Tìm x, biết 1 / 4 x = 16
A. x = -2 B. x = 2
C. x = 1/2 D. x = -1/2
Một chất điểm chuyển động đều với phương trình quỹ đạo\(\dfrac{x^2}{a^2}\) +\(\dfrac{x^2}{b^2}\)=1 (a và b là hằng số dương). Tìm bán kính quỹ đạo tại điểm x=0.
A.R=ab B.R=2ab C.R=\(\sqrt{a^2+b^2}\) D.R=\(\dfrac{a^2}{b}\)
Tính tích phân I=\(\int\limits^{\pi}_0\)\(x^2cos2xdx\) bằng cách đặt \(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\).Mệnh đề nào dưới đây đúng?
A. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-\int\limits^{\pi}_0xsin2xdx\)
B. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-2\int\limits^{\pi}_0xsin2xdx\)
C. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+\int\limits^{\pi}_0xsin2xdx\)
D. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+2\int\limits^{\pi}_0xsin2xdx\)
Cho hàm số y = f ( x ) liên tục trên R \ { - 1 ; 0 } thỏa mãn f ( 1 ) = 2 ln 2 + 1 , x ( x + 1 ) f ' ( x ) + ( x + 2 ) f ( x ) = x ( x + 1 ) , ∀ x ∈ R \ { - 1 ; 0 } Biết f ( 2 ) = a + b ln 3 với a, b là hai số hữu tỉ. Tính T = a 2 - b
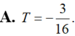
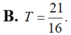
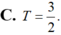
![]()
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
![]()
![]()
![]()
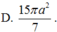
Biết\(I=\int\limits^5_2\dfrac{\left|x-2\right|}{x}dx=aln2+bln5+c\) với \(a,b,c\in Z\).Tìm \(a,b,c\)
Biết kết quả tích phân\(I=\)\(\int\limits^{\dfrac{\pi}{2}}_{\dfrac{\pi}{6}}\dfrac{\cos x}{\sin x+1}dx=aln2+bln3\) với \(a,b\) nguyên.Gía trị của \(H=a.b\) là