Câu 2:
\(\left|\overrightarrow{a}\right|=10\)
Câu 2:
\(\left|\overrightarrow{a}\right|=10\)
Cho hai vec tơ a→ và b→ có a → = 3 , b → = 3 , a → , b → = 120 ° . Với giá trị nào của m thì hai vec tơ a → + m b → v à a → - m b → vuông góc với nhau?
Cho hai điểm A(1; 0) và B( 0 ;-2). Vec tơ đối của vectơ A B → có tọa độ là:
A. (-1; 2).
B. (-1; -2).
C. (1;2).
D. (1; -2).
Trong mặt phẳng tọa độ cho hai vectơ a → 1 ; m , b → 3 ; 1 . Góc giữa hai vectơ a → , b → bằng 60 ° khi và chỉ khi
A. m = √ 3 / 3
B. m = 1 / 3
C. m = ( - √ 3 ) / 3
D. m = ( - 1 ) / 3
Cho tam giác đều ABC . Gọi M,N ,P lần lượt là các điểm thoả mãn vectơ BM = k vectơ BC , 4 vectơ AN = 3 vectơ AB , 3 vectơ AP = 2 vectơ AC . a, Biểu diễn vectơ AM theo hai vectơ AB , AC . b, Tìm k để hai đường thẳng AM , NP vuông góc với nhau.
Cho tam giác ABC với A = (1; 4), B = (2; – 5 ), C = (0; 7). Điểm M nằm trên trục Ox sao cho vectơ M A → + M B → + M C → có độ dài nhỏ nhất. Tọa độ điểm M là:
A. M(5; 0)
B. M(–2; 0)
C. M(3; 0)
D. M(1; 0)
Trong mặt phẳng tọa độ Oxy, cho hai vectơ u → = 4 ; 1 và v → = 1 ; 4 . Tìm m để vectơ a → = m . u → + v → tạo với vectơ b → = i → + j → một góc 450.
A. m = 4
B.m = -1/2
C.m = -1/4
D.m = 1/2
Trong phương vuông góc với Tọa độ Oxy, cho parabol (P): y = x² - 4mx + 3m² + 1, điểm A (0;3m) và đường thẳng (d): y = 2x + 3m-2 với m là tham số. Giả sử giao điểm của (d) và (P) là hai điểm M và N thì diện tích tam giác AMN bằng 4. Tìm giá trị của m
Cho hai tập khác rỗng : A = (m – 1; 4], B = (-2; 2m + 2), với m ∈ ℝ . Giá trị m để A ∩ B ⊂ (-1; 3) là:
A. m > 0
B. m < 1 2
C. 0 < m < 1 2
D. 0 ≤ m ≤ 1 2
Trên trục (O, e→) cho các điểm A, B, M, N có tọa độ lần lượt là -1, 2, 3, -2
a) Hãy vẽ trục và biểu diễn các điểm đã cho trên trục;
b) Tính độ dài đại số của 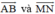 . Từ đó suy ra hai vec tơ
. Từ đó suy ra hai vec tơ 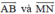 ngược hướng.
ngược hướng.