Question

1. cho A(2;-2), B(4;1), C(0;3). Tính tọa độ điểm D để ABCD là hình bình hành

2. cho A(7;2), B(1;-1), C(4;6). Tính tọa độ điểm D để ABCD là hình bình hành

Answer 1

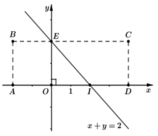
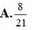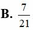1:

ABCD là hình bình hành

=>\(\overrightarrow{AB}=\overrightarrow{DC}\)

mà \(\overrightarrow{AB}=\left(2;1\right);\overrightarrow{DC}=\left(-x;3-y\right)\)

nên \(\left\{{}\begin{matrix}-x=2\\3-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=2\end{matrix}\right.\)

Vậy: D(-2;2)

2: ABCD là hình bình hành

=>\(\overrightarrow{AB}=\overrightarrow{DC}\)

mà \(\overrightarrow{AB}=\left(-6;-3\right);\overrightarrow{DC}=\left(4-x;6-y\right)\)

nên \(\left\{{}\begin{matrix}4-x=-6\\6-y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=9\end{matrix}\right.\)

Vậy: D(10;9)

Answer 2

ABCD là hình bình hành khi \(\overrightarrow{AB}=\overrightarrow{DC}\)

Gọi D(x;y)

a.

\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(2;3\right)\\\overrightarrow{DC}=\left(-x;3-y\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-x=2\\3-y=3\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\) \(\Rightarrow D\left(-2;0\right)\)

b.

\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-6;-3\right)\\\overrightarrow{DC}=\left(4-x;6-y\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4-x=-6\\6-y=-3\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=10\\y=9\end{matrix}\right.\) \(\Rightarrow D\left(10;9\right)\)

Answer 3

`1. D = (2 + 0 - 4 ; -2 + 3 - 1) = (-2;0)`

`2. D = (7+4-1 ; 2+6-(-1)) = (10;9)`