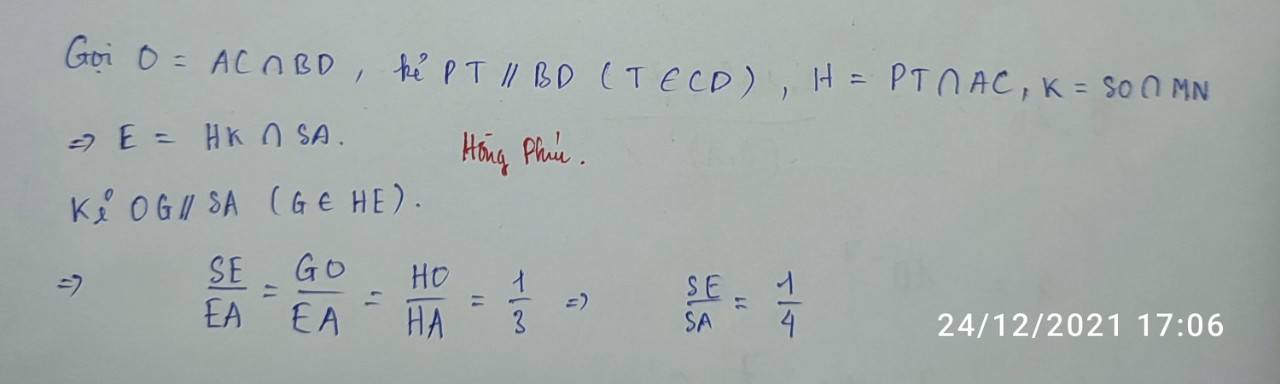Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M, N, E lần lượt là trung điểm của SA, SB, SD. Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
Xem chi tiết
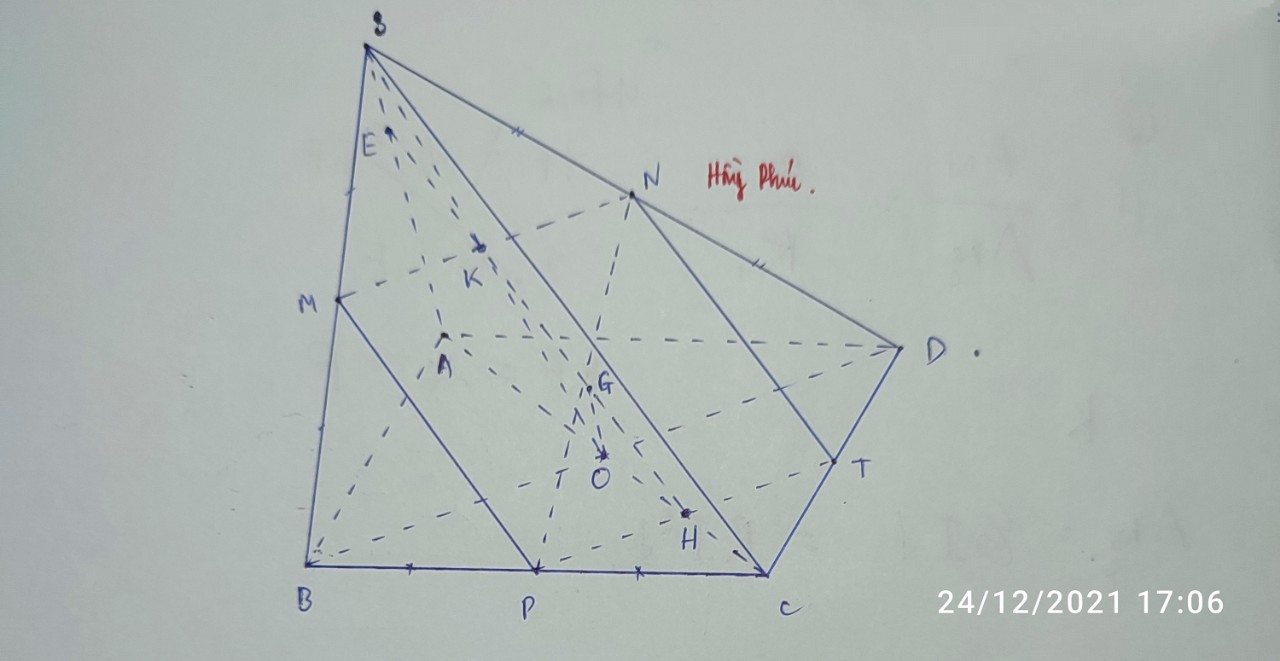
Cho hình chóp SABCD , đáy là hình bình hành tâm O. Gọi M , N , P lần lượt là trung điểm SB , SD và OC a) Tìm giao tuyên (MNP) với ( SAC) , tìm giao điểm (MNP) với SA b ) Xác định thiết diện của hình chóp với (MNP) và tìm tỉ số mà (MNP) chia các cạnh SA , BC , CD
Cho hình chóp S.ABCD có đáy abcd là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CD, SD
1. Xác định giao tuyến của (SAC) ; (SBD) và chứng minh NP song song với (SBC)
2.Gọi Q là giao điểm của SA với (MNP). Tính tỉ số \(\dfrac{SQ}{SA}\)
Cho hình chóp S.ABCD có đáy abcd là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CD, SD
1. Xác định giao tuyến của (SAC) ; (SBD) và chứng minh NP song song với (SBC)
2.Gọi Q là giao điểm của SA với (MNP). Tính tỉ số \(\dfrac{SQ}{SA}\)
Cho khối chóp S.ABCD có đáy là hình bình hành, AB3, AD4,
B
A
D
^
120
o
Cạnh bên SA
2
3
vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳn...
Đọc tiếp
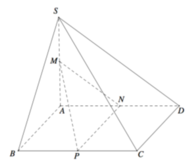
Cho khối chóp S.ABCD có đáy là hình bình hành, AB=3, AD=4, B A D ^ = 120 o Cạnh bên SA= 2 3 vuông góc với đáy. Gọi M,N,P lần lượt là trung điểm các cạnh SA, AD và BC (tham khảo hình vẽ bên). Tính góc giữa hai mặt phẳng (SBC) và (MNP).
A. 60 o
B. 45 o
C. 90 o
D. 30 o
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm 0; cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA=a. Gọi M,N lần lượt là trung điểm của SD và BC. Tính khoảng cách từ điểm M đến mặt phẳng (SBC)
cho hình chóp SABCD đáy ABCD là hình chữ nhật AB= a ,AD=2a,SA=SB=SC=SD=2a gọi O là giao điểm của AC và BD
a chứng minh mặt phẳng SAC vuông góc với mặt phẳng ABCD
b tính khoảng cách từ O->mặt phẳng SCD
c gọi M,N lần lượt là trung điểm của các cạnh SA và BC tính sin góc MN,CSBD
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm SA,N là điểm thuộc cạnh SB sao cho SN=2NB.
a)Tìm giao điểm P của MN với mặt phẳng (ABCD)
b) Chứng minh PC // (SBD)
c) Gọi H là giao điểm cảu (NPC) với SD và G là trọng tâm của tam giác SCD. Chứng minh (NHG) // (ABCD)
Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Các cạnh bên SA = SB = SC = SD = a√2. Gọi I và K lần lượt là trung điểm của AD và BC.
a) Chứng minh mặt phẳng (SIK) vuông góc với mặt phẳng (SBC).
b) Tính khoảng cách giữa hai đường thẳng AD và SB.