Đáp án B
Ta có
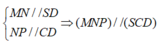
![]()
Tính được
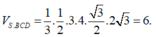
Ta có
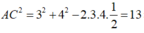
![]()
Tam giác SBC có
![]()
![]()
Tam giác
![]()
![]()
Vì vậy
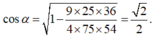
Đáp án B
Ta có
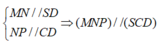
![]()
Tính được
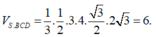
Ta có
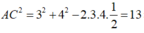
![]()
Tam giác SBC có
![]()
![]()
Tam giác
![]()
![]()
Vì vậy
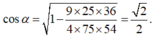
Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Các cạnh bên SA = SB = SC = SD = a√2. Gọi I và K lần lượt là trung điểm của AD và BC.
a) Chứng minh mặt phẳng (SIK) vuông góc với mặt phẳng (SBC).
b) Tính khoảng cách giữa hai đường thẳng AD và SB.
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45 0 . Gọi M, N lần lượt là trung điểm của AB, AD. Tính thể tích khối chóp S.CDMN theo a
A . 5 a 3 8
B . a 3 8
C . 5 a 3 24
D . a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2 3 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi M, N, P lần lượt là trung điểm của các cạnh SA, CD, CB. Tính côsin góc tạo bởi mặt phẳng (MNP) và (SCD).
A. 2 435 145
B. 11 435 145
C. 2 870 145
D. 3 145 145
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm 0; cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA=a. Gọi M,N lần lượt là trung điểm của SD và BC. Tính khoảng cách từ điểm M đến mặt phẳng (SBC)
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M; N’; P lần lượt là trung điểm của các cạnh BC; CD và SA. Gọi E là giao điểm của MN và AD; F là giao điểm của MN và AB. Tìm giao tuyến của (MNP) và (SBC)
A. ME
B. MH trong đó H là giao điểm của SD và PE
C. MK trong đó K là giao điểm của SB và PF
D. đáp án khác
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB =a, AD = 2a Cạnh bên SA vuông góc với mặt phẳng đáy và cạnh bên SC tạo với đáy một góc 60 o Gọi M, N là trung điểm các cạnh bên SA và SB Khoảng cách từ điểm S đến mặt phẳng (DMN) bằng
A. 2 a 465 31
B. a 31 31
C. a 60 31
D. 2 a 5 31
cho hình chóp SABCD đáy ABCD là hình chữ nhật AB= a ,AD=2a,SA=SB=SC=SD=2a gọi O là giao điểm của AC và BD
a chứng minh mặt phẳng SAC vuông góc với mặt phẳng ABCD
b tính khoảng cách từ O->mặt phẳng SCD
c gọi M,N lần lượt là trung điểm của các cạnh SA và BC tính sin góc MN,CSBD
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng 2, cạnh bên SA bằng 3 và vuông góc với mặt phẳng đáy. Gọi M là trung điểm của cạnh bên SB và N là hình chiếu vuông góc của A trên SO. Mệnh đề nào sau đây đúng?
A. A C ⊥ S D O
B. A M ⊥ S D O
C. S A ⊥ S D O
D. A N ⊥ S D O
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, A D = a 6 , A B = a 3 ; M là trung điểm cạnh AD, hai mặt phẳng (SAC) và (SBM) cùng vuông góc với đáy; SA tạo với đáy góc 60 0 . Tính theo a thể tích khối chóp S.OMC.
A . a 3 6 8
A . 3 a 3 6 8
C . a 3 3 4
D . 3 a 3 3 4