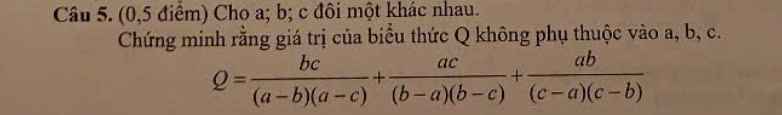Ta có: \(Q=\dfrac{bc}{\left(a-b\right)\left(a-c\right)}+\dfrac{ac}{\left(b-a\right)\left(b-c\right)}+\dfrac{ab}{\left(c-a\right)\left(c-b\right)}\)
\(=\dfrac{bc}{\left(a-b\right)\left(a-c\right)}-\dfrac{ac}{\left(a-b\right)\left(b-c\right)}+\dfrac{ab}{\left(a-c\right)\left(b-c\right)}\)
\(=\dfrac{bc\left(b-c\right)-ac\left(a-c\right)+ab\left(a-b\right)}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}\)
\(=\dfrac{b^2c-bc^2-a^2c+ac^2+ab\left(a-b\right)}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}\)
\(=\dfrac{c\left(b^2-a^2\right)+c^2\left(a-b\right)+ab\left(a-b\right)}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}\)
\(=\dfrac{-c\left(a-b\right)\left(a+b\right)+c^2\left(a-b\right)+ab\left(a-b\right)}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}\)
\(=\dfrac{\left(a-b\right)\left(-ca-cb+c^2+ab\right)}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}\)
\(=\dfrac{c^2-ca-cb+ab}{\left(a-c\right)\left(b-c\right)}=\dfrac{c\left(c-a\right)-b\left(c-a\right)}{\left(a-c\right)\left(b-c\right)}\)
\(=\dfrac{\left(c-a\right)\left(c-b\right)}{\left(c-a\right)\left(c-b\right)}=1\)
=>Q không phụ thuộc vào biến