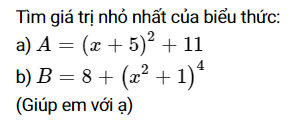a.
Do \(\left(x+5\right)^2\ge0;\forall x\)
Dấu '=" xảy ra khi \(x+5=0\Rightarrow x=-5\)
Nên \(\left(x+5\right)^2+11\ge11\) với mọi x
Vậy \(A_{min}=11\) khi `x=-5`
b.
Do \(x^2\ge0;\forall x\)
Dấu "=" xảy ra khi `x=0`
Nên \(x^2+1\ge1;\forall x\)
Hay \(\left(x^2+1\right)^4\ge1;\forall x\)
Suy ra \(8+\left(x^2+1\right)^2\ge9;\forall x\)
Vậy \(B_{min}=9\) khi `x=0`
`A = (x+5)^2 + 11`
Do ` (x+5)^2 >= 0` với mọi x
`=> (x+5)^2 + 11 >= 11` với mọi x
`=> A >= 11`
Dấu = có khi:
`x + 5 = 0`
`=> x = -5`
Vậy ....
``
`B = 8 + (x^2 + 1)^4 `
B đạt GTNN khi: `(x^2 + 1)^4` đạt GTNN
Thấy `x^2 + 1 > 0`
`=> x^2 + 1` đạt giá trị nhỏ nhất
`=> x^2 = 0`
`=> x = 0`
Khi đó `B = 8 + 1^4 = 9`
Vậy ....