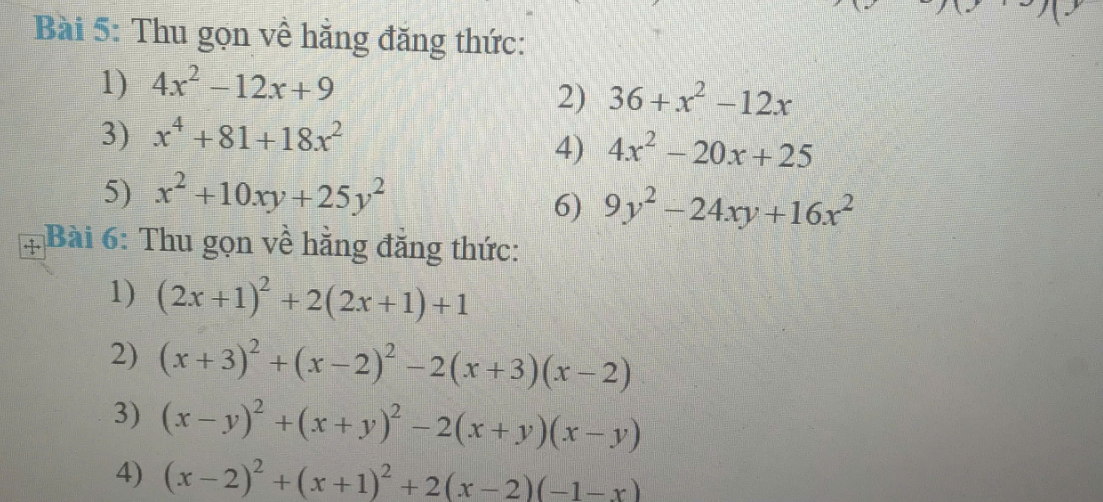Bài 5:
1: \(4x^2-12x+9=\left(2x\right)^2-2\cdot2x\cdot3+3^2=\left(2x-3\right)^2\)
3: \(x^4+81+18x^2=\left(x^2\right)^2+2\cdot x^2\cdot9+9^2=\left(x^2+9\right)^2\)
5: \(x^2+10xy+25y^2=x^2+2\cdot x\cdot5y+\left(5y\right)^2=\left(x+5y\right)^2\)
2: \(36+x^2-12x=x^2-2\cdot x\cdot6+6^2=\left(x-6\right)^2\)
4: \(4x^2-20x+25=\left(2x\right)^2-2\cdot2x\cdot5+5^2=\left(2x-5\right)^2\)
6: \(9y^2-24xy+16x^2\)
\(=\left(3y\right)^2-2\cdot3y\cdot4x+\left(4x\right)^2\)
\(=\left(3y-4x\right)^2\)
Bài 6:
1: \(\left(2x+1\right)^2+2\left(2x+1\right)+1\)
\(=\left(2x+1\right)^2+2\cdot\left(2x+1\right)\cdot1+1^2\)
\(=\left(2x+1+1\right)^2=\left(2x+2\right)^2\)
2: \(\left(x+3\right)^2+\left(x-2\right)^2-2\left(x+3\right)\left(x-2\right)\)
\(=\left(x+3\right)^2-2\left(x+3\right)\left(x-2\right)+\left(x-2\right)^2\)
\(=\left(x+3-x+2\right)^2=5^2=25\)
3: \(\left(x-y\right)^2+\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)\)
\(=\left(x-y\right)^2-2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\)
\(=\left(x-y-x-y\right)^2=\left(-2y\right)^2=4y^2\)
4: \(\left(x-2\right)^2+\left(x+1\right)^2+2\left(x-2\right)\left(-1-x\right)\)
\(=\left(x-2\right)^2-2\cdot\left(x-2\right)\left(x+1\right)+\left(x+1\right)^2\)
\(=\left(x-2-x-1\right)^2=\left(-3\right)^2=9\)
Bài tập mẫu `1:`
\(a,\left(3x+5\right)^2=\left(3x\right)^2+2\cdot3x\cdot5+5^2\\ =9x^2+30x+25\\ b,\left(2x-1\right)^2=\left(2x\right)^2-2\cdot2x\cdot1+1^2\\ =4x^2-4x+1\\ c,\left(3x+2y\right)^2=\left(3x\right)^2+3x\cdot2y\cdot2+\left(2y\right)^2\\ =9x^2+12xy+4y^2\)
Bài tập mẫu `2:`
\(a,\left(a+\dfrac{1}{4}\right)^2\\ =a^2+a\cdot2\cdot\dfrac{1}{2}+\dfrac{1}{2}\\ =a^2+a+\dfrac{1}{2}\\ b,\left(\dfrac{1}{2}x-\dfrac{2}{3}\right)^2\\ =\left(\dfrac{1}{2}x\right)^2-2\cdot\dfrac{1}{2}x\cdot\dfrac{2}{3}+\left(\dfrac{2}{3}\right)^2\\ =\dfrac{1}{4}x^2-\dfrac{2}{3}x+\dfrac{4}{9}\\ c,\left(\dfrac{1}{3}x+\dfrac{3}{2}y\right)^2\\ =\left(\dfrac{1}{3}x\right)^2+2\cdot\dfrac{1}{3}x\cdot\dfrac{3}{2}y+\left(\dfrac{3}{2}y\right)^2\\ =\dfrac{1}{9}x^2+xy+\dfrac{9}{4}y^2\)