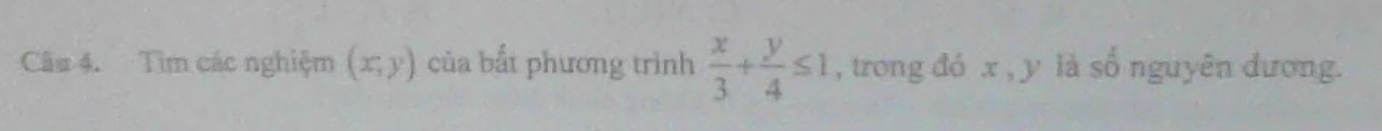\(\dfrac{x}{3}+\dfrac{y}{4}\le1\)
\(\Leftrightarrow4x+3y\le12\)
\(x\in Z^+;y\in Z^+\)
Từ đồ thị ta thấy \(\left(x;y\right)=\left(1;1\right);\left(2;1\right);\left(1;2\right)\) thỏa mãn đề bài
\(\dfrac{x}{3}+\dfrac{y}{4}\le1\Leftrightarrow\dfrac{4x+3y}{12}\le1\Leftrightarrow4x+3y\le12\left(1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}4x\le12\\3y\le12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le3\\y\le4\end{matrix}\right.\)
mà x,y là các số nguyên dương
\(\Rightarrow\left\{{}\begin{matrix}1\le x\le3\\1\le y\le4\end{matrix}\right.\)
Xét từng cặp giá trị x,y với nhau, ta thấy \(\left(x;y\right)=\left\{\left(1;1\right);\left(1;2\right);\left(2;1\right)\right\}\) thỏa mãn (1) và yêu cầu của đề bài