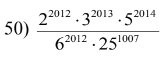\(\dfrac{2^{2012}\cdot3^{2013}\cdot5^{2014}}{6^{2012}\cdot25^{1007}}=\dfrac{2^{2012}\cdot3^{2012}\cdot3\cdot5^{2014}}{2^{2012}\cdot3^{2012}\cdot\left(5^2\right)^{1007}}=\dfrac{3\cdot5^{2014}}{5^{2014}}=3\)
`(2^2012 . 3^2013 . 5^2014)/(6^3012 . 25^1007)`
`= (2^2012 . 3^2013 . 5^2014)/(2^2012 . 3^2012 . 5^2014)`
`= (1 . 3 . 1)/(1 . 1 . 1)`
`= 3`
\(50,\dfrac{2^{2012}.3^{2013}.5^{2014}}{6^{2012}.25^{1007}}=\dfrac{2^{2012}.3^{2013}.5^{2014}}{\left(2.3\right)^{2012}.\left(5^2\right)^{1007}}=\dfrac{2^{2012}.3^{2013}.5^{2014}}{2^{2012}.3^{2012}.5^{2014}}=3\)
\(\dfrac{2^{2012}\cdot3^{2013}\cdot5^{2014}}{6^{2012}\cdot25^{1007}}\)
\(=\dfrac{2^{2012}\cdot3^{2013}\cdot5^{2014}}{\left(3\cdot2\right)^{2012}\cdot\left(5^2\right)^{1007}}\)
\(=\dfrac{2^{2012}\cdot3^{2013}\cdot5^{2014}}{3^{2012}\cdot2^{2012}\cdot5^{2014}}\)
\(=\dfrac{1\cdot3\cdot1}{1\cdot1\cdot1}\)
\(=3\)