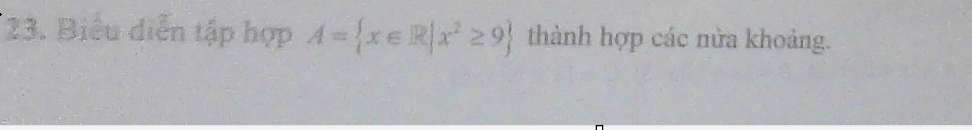\(x^2>=9\)
=>\(\left[{}\begin{matrix}x>=3\\x< =-3\end{matrix}\right.\)
=>A=[3;+\(\infty\))\(\cup\)(-\(\infty\);-3]
Để biểu diễn tập hợp \( A = \{ x \in \mathbb{R} \mid x^2 \geqslant 9 \} \) thành hợp các nửa khoảng, ta cần tìm các giá trị của \( x \) thỏa mãn điều kiện \( x^2 \geqslant 9 \).
Điều kiện \( x^2 \geqslant 9 \) tương đương với \( |x| \geqslant 3 \), tức là \( x \leqslant -3 \) hoặc \( x \geqslant 3 \).
Vậy, tập hợp \( A \) có thể biểu diễn bằng hợp các nửa khoảng như sau:
\[ A = (-\infty, -3] \cup [3, +\infty) \]
Do đó, tập hợp \( A \) được biểu diễn thành hợp các nửa khoảng là \( (-\infty, -3] \cup [3, +\infty) \).