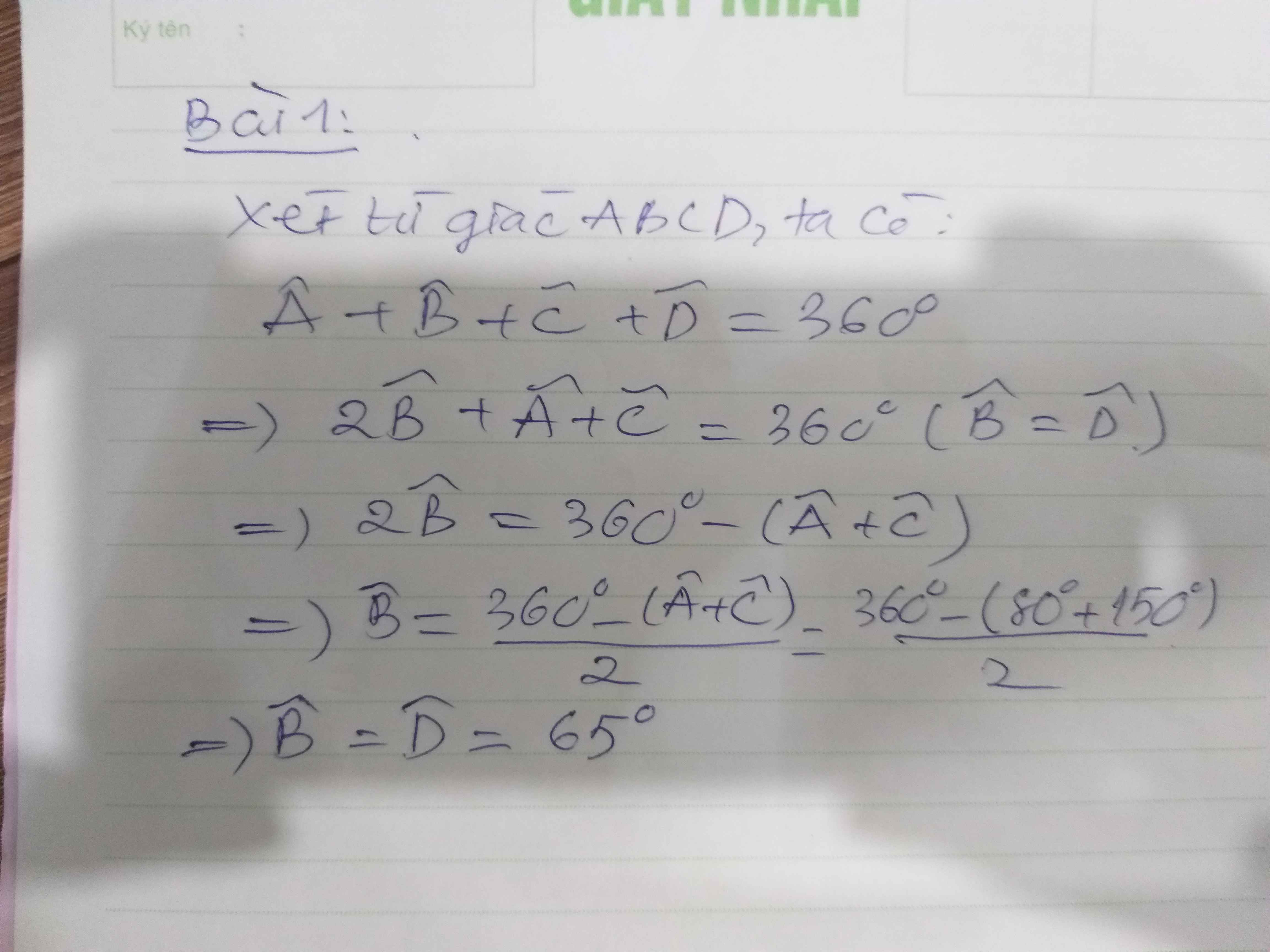Bài 1: Xét tứ giác ABCD có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
=>\(\widehat{B}+\widehat{D}=360^0-150^0-80^0=130^0\)
mà \(\widehat{B}=\widehat{D}\)
nên \(\widehat{B}=\widehat{D}=\dfrac{130^0}{2}=65^0\)
Bài 2:
a: Ta có: AB//CD
M\(\in\)CD
Do đó: AB//MD
Ta có: AB=CD/2
\(MD=MC=\dfrac{CD}{2}\)
Do đó: AB=MD=MC
Xét tứ giác ABMD có
AB//MD
AB=MD
Do đó: ABMD là hình bình hành
b: ABMD là hình bình hành
=>BM//AD và BM=AD
Ta có: BM//AD
K\(\in\)AD
Do đó: BM//AK
Ta có: BM=AD
AD=AK
Do đó: BM=AK
Xét tứ giác AMBK có
BM//AK
BM=AK
Do đó: AMBK là hình bình hành
Bài 3:
a: Ta có: AB//DC
E\(\in\)AB
Do đó: BE//DC
Ta có:AB=DC
AB=BE
Do đó: BE=DC
Xét tứ giác DBEC có
BE//DC
BE=DC
Do đó: DBEC là hình bình hành
b: Ta có: AD//BC
F\(\in\)AD
Do đó: DF//BC
Ta có: AD=BC
AD=DF
Do đó: DF=BC
Xét tứ giác DBCF có
DF//BC
DF=BC
Do đó: DBCF là hình bình hành
=>DB//CF và DB=CF
Ta có: DBEC là hình bình hành
=>DB//CE và DB=CE
Ta có: DB//CE
DB//CF
mà CE,CF có điểm chung là C
nên F,E,C thẳng hàng
Ta có: DB=CE
DB=CF
Do đó: CE=CF
mà F,E,C thẳng hàng
nên C là trung điểm của EF
c: Xét ΔAFE có
AC,FB,ED là các đường trung tuyến
Do đó: AC,FB,ED đồng quy