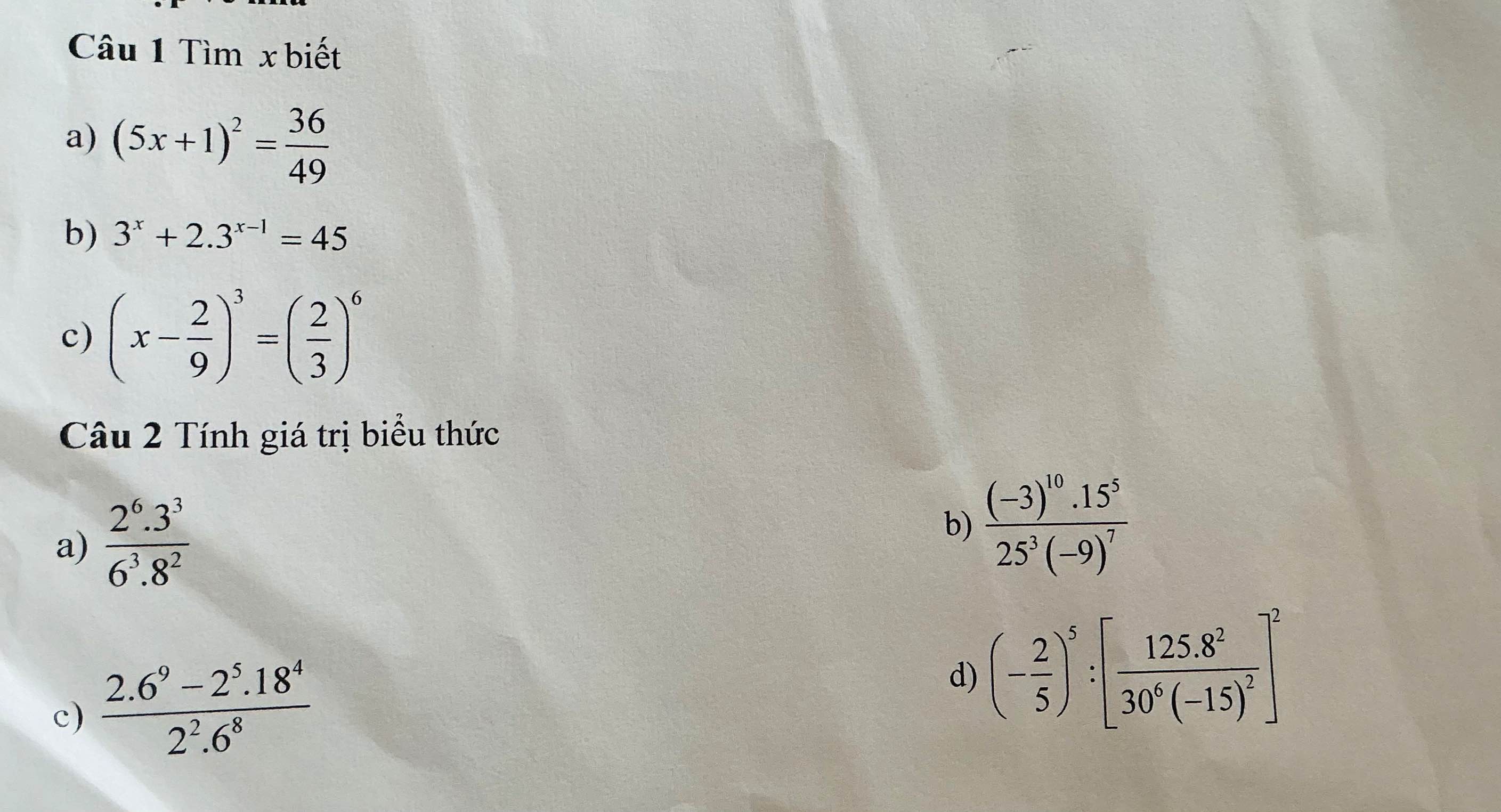\(C1:\\ a)\left(5x+1\right)^2=\dfrac{36}{49}\\ =>\left(5x+1\right)^2=\left(\dfrac{6}{7}\right)^2\\ TH1:5x+1=\dfrac{6}{7}\\ =>5x=\dfrac{6}{7}-1=-\dfrac{1}{7}\\ =>x=-\dfrac{1}{7}:5\\ =>x=-\dfrac{1}{35}\\ TH2:5x+1=-\dfrac{6}{7}\\ =>5x=-\dfrac{6}{7}-1=-\dfrac{13}{7}\\ =>x=-\dfrac{13}{7}:5=-\dfrac{13}{35}\\ b)3^x+2\cdot3^{x-1}=45\\ =>3^{x-1}\cdot\left(3+2\right)=45\\ =>3^{x-1}\cdot5=45\\ =>3^{x-1}=45:5\\ =>3^{x-1}=9\\ =>3^{x-1}=3^2\\ =>x-1=2\\ =>x=3\\ c,\left(x-\dfrac{2}{9}\right)^3=\left(\dfrac{2}{3}\right)^6\\ =>\left(x-\dfrac{2}{9}\right)^3=\left[\left(\dfrac{2}{3}\right)^2\right]^3\\ =>x-\dfrac{2}{9}=\dfrac{4}{9}\\ =>x=\dfrac{4}{9}+\dfrac{2}{9}=\dfrac{6}{9}=\dfrac{2}{3}\)
Câu 4 :
a) \(7^6+7^5-7^4=7^4\left(7^2+7-1\right)=7^4.55=7^4.5.11⋮11\Rightarrowđpcm\)
b) \(2^{100}+2^{101}+2^{102}=2^{100}\left(1+2+2^2\right)=2^{100}.7=2^{99}.2.7=2^{99}.14⋮14\Rightarrowđpcm\)
Câu 5 :
\(A=3^2+6^2+9^2+...+30^2\)
\(\Rightarrow A=3^2.1^2+3^2.2^2+3^2.3^2+...+3^2.10^2\)
\(\Rightarrow A=3^2.\left(1^2+2^2+3^2+...+10^2\right)\)
mà \(1^2+2^2+3^2+...+10^2=385\)
\(\Rightarrow A=3^2.385=9.385=3465\)
Câu 2:
a: \(\dfrac{2^6\cdot3^3}{6^3\cdot8^2}=\dfrac{2^6\cdot3^2}{2^6\cdot2^3\cdot3^3}=\dfrac{1}{8\cdot3}=\dfrac{1}{24}\)
b: \(\dfrac{\left(-3\right)^{10}\cdot15^3}{25^3\cdot\left(-9\right)^7}=\dfrac{3^{10}\cdot3^3\cdot5^3}{5^6\cdot\left(-1\right)\cdot3^{14}}=-\dfrac{1}{3}\cdot\dfrac{1}{5^3}=-\dfrac{1}{375}\)
c: \(\dfrac{2\cdot6^9-2^5\cdot18^4}{2^2\cdot6^8}=\dfrac{2^{10}\cdot3^9-2^5\cdot2^4\cdot3^8}{2^2\cdot2^8\cdot3^8}\)
\(=\dfrac{2^{10}\cdot3^9-2^9\cdot3^8}{2^{10}\cdot3^8}=\dfrac{2^9\cdot3^8\left(2\cdot3-1\right)}{2^{10}\cdot3^8}\)
\(=\dfrac{1}{2}\cdot\dfrac{6-1}{1}=\dfrac{5}{2}\)
d: \(\left(-\dfrac{2}{5}\right)^5:\left[\dfrac{125\cdot8^2}{30^6\cdot\left(-15\right)^2}\right]^2\)
\(=\dfrac{\left(-2\right)^5}{5^5}:\left[\dfrac{5^3\cdot2^6}{5^6\cdot2^6\cdot3^6\cdot5^2\cdot3^2}\right]^2\)
\(=\dfrac{\left(-2\right)^5}{5^5}:\left[\dfrac{1}{5^5}\cdot\dfrac{1}{3^8}\right]^2\)
\(=\dfrac{\left(-2\right)^5}{5^5}\cdot\dfrac{5^{10}\cdot3^{16}}{1}=\left(-2\right)^5\cdot5^5\cdot3^{16}\)
Câu 3:
a: \(\left(\dfrac{1}{2}\right)^8:\left(\dfrac{1}{2}\right)^2=\left(\dfrac{1}{2}\right)^6;\left(\dfrac{1}{2}\right)^3\cdot\left(\dfrac{1}{2}\right)^3=\left(\dfrac{1}{2}\right)^6\)
Do đó: \(\left(\dfrac{1}{2}\right)^8:\left(\dfrac{1}{2}\right)^2=\left(\dfrac{1}{2}\right)^3\cdot\left(\dfrac{1}{2}\right)^3\)
b: \(8^{12}=\left(8^3\right)^4=512^4\)
\(12^8=\left(12^2\right)^4=144^4\)
mà 512>144
nên \(8^{12}>12^8\)
c: \(\dfrac{8^{10}\cdot3^{30}}{7^{30}\cdot4^{15}}=\dfrac{8^{10}}{4^{15}}\cdot\dfrac{3^{30}}{7^{30}}=\dfrac{2^{30}}{2^{30}}\cdot\dfrac{9^{15}}{7^{30}}=\dfrac{9^{15}}{7^{30}}>\dfrac{4^{15}}{7^{30}}\)