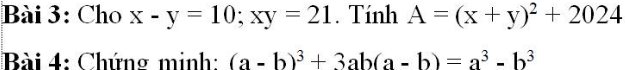Bài 3:
Ta có:
`x - y = 10`
`=> (x-y)^2 = 100`
`=> x^2 - 2xy + y^2 = 100`
`=> x^2 + 2xy + y^2 - 4xy = 100`
`=> (x+y)^2 - 4 . 21 = 100`
`=> (x+y)^2 - 84 = 100`
`=> (x+y)^2 = 184`
Khi đó: `(x+y)^2 + 2024 = 184 + 2024 = 2208`
Bài 4:
`(a-b)^3 + 3ab (a-b) = a^3 - b^3`
```<=> a^3 - 3a^2 b + 3ab^2 - b^3 + 3a^2 b - 3ab^2 = a^3 - b^3`
`<=> (a^3 - b^3) + (3ab^2 - 3ab^2)+ (3a^2 b - 3a^2 b) = a^3 - b^3`
`<=> (a^3 - b^3) + 0+0= a^3 - b^3`
`<=> a^3 - b^3= a^3 - b^3` (Luôn đúng)
3.
\(A=\left(x+y\right)^2+2024=x^2+2xy+y^2+2024\)
\(=\left(x^2-2xy+y^2\right)+4xy+2024\)
\(=\left(x-y\right)^2+4xy+2024\)
\(=10^2+4.21+2024=2208\)
4.
\(\left(a-b\right)^3+3ab\left(a-b\right)=a^3-3a^2b+3ab^2-b^3+3a^2b-3ab^2\)
\(=a^3-b^3\)