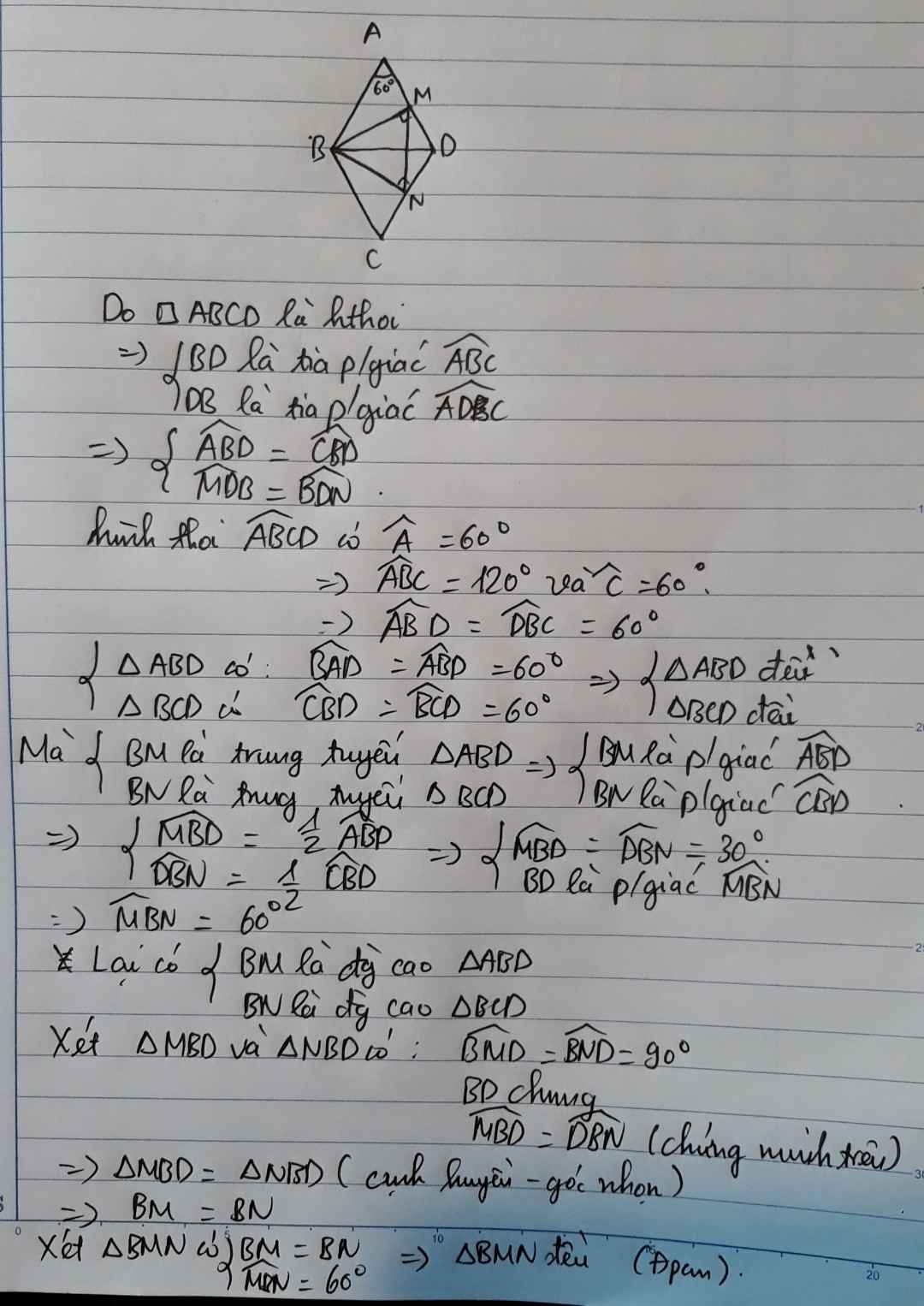Ta có: \(AM=DM=\dfrac{AD}{2}\)
\(CN=DN=\dfrac{CD}{2}\)
mà AD=CD
nên AM=DM=CN=DN
Xét ΔBAM và ΔBCN có
BA=BC
\(\widehat{BAM}=\widehat{BCN}\)
AM=CN
Do đó: ΔBAM=ΔBCN
=>BM=BN
Xét ΔABD có AB=AD và \(\widehat{BAD}=60^0\)
nên ΔABD đều
ΔBAD đều
mà BM là đường trung tuyến
nên BM\(\perp\)AD tại M
Xét ΔBCD có CB=CD và \(\widehat{BCD}=60^0\)
nên ΔBCD đều
ΔBCD đều
mà BN là đường trung tuyến
nên BN\(\perp\)CD
ABCD là hình thoi
=>\(\widehat{ADC}+\widehat{BCD}=180^0\)
=>\(\widehat{ADC}=120^0\)
Xét tứ giác BMDN có \(\widehat{BMD}+\widehat{BND}+\widehat{MBN}+\widehat{MDN}=360^0\)
=>\(\widehat{MBN}=360^0-90^0-90^0-120^0=60^0\)
Xét ΔBMN có BM=BN và \(\widehat{MBN}=60^0\)
nên ΔBMN đều