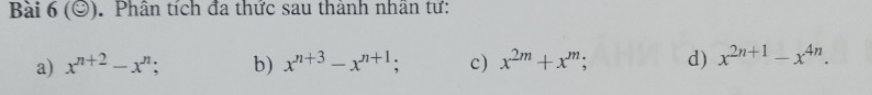`a)x^{n+2}-x^n=x^n(x^2-1)=x^n(x-1)(x+1)`
`b)x^{n+3}-x^{n+1}=x^{n+1}(x^2-1)=x^{n+1}(x-1)(x+1)`
`c)x^{2m}+x^m=x^m(x^m+1)`
`d)x^{2n+1}-x^{4n}=x^{2n+1}(1-x^{2n-1})`
a: \(x^{n+2}-x^n\)
\(=x^n\cdot x^2-x^n\cdot1\)
\(=x^n\left(x^2-1\right)=x^n\left(x-1\right)\left(x+1\right)\)
b: \(x^{n+3}-x^{n+1}\)
\(=x^n\cdot x^3-x^n\cdot x\)
\(=x^n\left(x^3-x\right)\)
\(=x^n\cdot x\left(x^2-1\right)=x^{n+1}\cdot\left(x-1\right)\left(x+1\right)\)
c: \(x^{2m}+x^m\)
\(=\left(x^m\right)^2+x^m\)
\(=x^m\left(x^m+1\right)\)
d: \(x^{2n+1}-x^{4n}=x^{2n}\cdot x-x^{2n}\cdot x^{2n}\)
\(=x^{2n}\left(x-x^{2n}\right)=x^{2n+1}\left(1-x^{2n-1}\right)\)