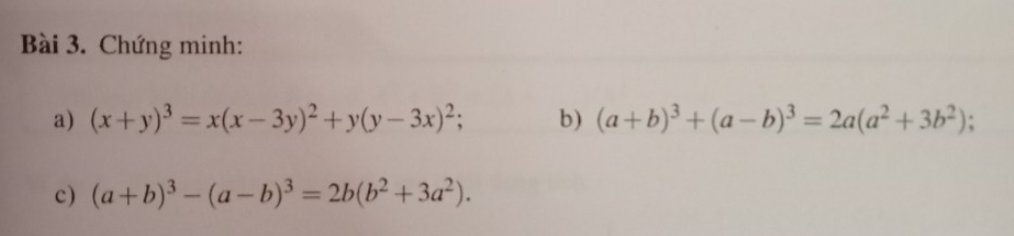a: VP=\(x\left(x-3y\right)^2+y\left(y-3x\right)^2\)
\(=x\left(x^2-6xy+9y^2\right)+y\left(9x^2-6xy+y^2\right)\)
\(=x^3-6x^2y+9xy^2+9x^2y-6xy^2+y^3\)
\(=x^3+3x^2y+3xy^2+y^3=\left(x+y\right)^3=VT\)
b: \(VT=\left(a+b\right)^3+\left(a-b\right)^3\)
\(=a^3+b^3+3a^2b+3ab^2+a^3-3a^2b+3ab^2-b^3\)
\(=2a^3+6ab^2=2a\left(a^2+3b^2\right)=VP\)
c: \(VT=\left(a+b\right)^3-\left(a-b\right)^3\)
\(=a^3+3a^2b+3ab^2+b^3-\left(a^3-3a^2b+3ab^2-b^3\right)\)
\(=a^3+3a^2b+3ab^2+b^3-a^3+3a^2b-3ab^2+b^3\)
\(=6a^2b+2b^3=2b\left(3a^2+b^2\right)=VP\)
a)
\(\left(x+y\right)^3=x^3+3x^2y+3xy^2+y^3\\ =\left(x^3-6x^2y+9xy^2\right)+\left(y^3-6xy^2+9x^2y\right)\\ =x\left(x^2-6xy+9y^2\right)+y\left(y^2-6xy+9x^2\right)\\ =x\left(x-3y\right)^2+y\left(y-3x\right)^2\left(đpcm\right)\)
b)
\(\left(a+b\right)^3+\left(a-b\right)^3=a^3+3a^2b+3ab^2+b^3+a^3-3a^2b+3ab^2-b^3\\ =2a^3+6ab^2\\ =2a\left(a^2+3b^2\right)\left(đpcm\right)\)
c)
\(\left(a+b\right)^3-\left(a-b\right)^3\\ =\left(a+b-a+b\right)\left[\left(a+b\right)^2+\left(a+b\right)\left(a-b\right)+\left(a-b\right)^2\right]\\ =2b\left(a^2+2ab+b^2+a^2-b^2+a^2-2ab+b^2\right)\\ =2b\left(3a^2+b^2\right)\left(đpcm\right)\)