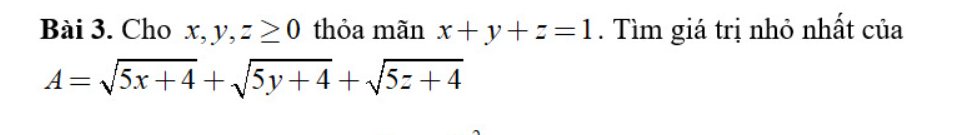Lời giải:
Do $x+y+z=1, x,y,z\geq 0$ nên $0\leq x, y, z\leq 1$.
Ta sẽ cm $\sqrt{5x+4}\geq x+2(*)$
Thật vậy:
BĐT $(*)\Leftrightarrow 5x+4\geq (x+2)^2$
$\Leftrightarrow 5x+4\geq x^2+4x+4$
$\Leftrightarrow x\geq x^2\Leftrightarrow x(1-x)\geq 0$ (luôn đúng với mọi $0\leq x\leq 1$)
$\Rightarrow$ BĐT $(*)$ luôn đúng.
Hoàn toàn tương tự:
$\sqrt{5y+4}\geq y+2; \sqrt{5z+4}\geq z+2$
Cộng các BĐT trên theo vế và thu gọn:
$\sqrt{5x+4}+\sqrt{5y+4}+\sqrt{5z+4}\geq x+y+z+6=1+6=7$
Vậy $A_{\min}=7$. Giá trị này đạt tại $(x,y,z)=(0,0,1)$ và hoán vị.