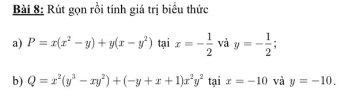a, \(P=x\left(x^2-y\right)+y\left(x-y^2\right)=x^3-xy+xy-y^3=x^3-y^3\)
Thay x = -1/2 ; y = -1/2
\(P=-\dfrac{1}{8}+\dfrac{1}{8}=0\)
b, \(Q=x^2y^3-x^3y^2-x^2y^3+x^3y^2+x^2y^2=x^2y^2\)
Thay x = -10 ; y = -10 ta được
\(10^2.10^2=10000\)
`a)P=x^3 - xy + xy - y^3`
`P=x^3 - y^3`
Thay `x=-1/2;y=-1/2` vào `P:`
`P=(-1/2)^3 - (-1/2)^3`
`P=-1/8 + 1/8`
`P=0`
Vậy khi `x=-1/2;y=-1/2` thì `P=0`
`b)Q=x^2 y^3 - x^3 y^2 - x^2 y^3 + x^3 y^2+ x^2 y^2`
`Q=(x^2 y^3 - x^2 y^3) + (-x^3 y^2 + x^3 y^2) + x^2 y^2`
`Q=x^2 y^2`
Thay `x=-10, y=-10` vào `Q:`
`Q=(-10)^2 . (-10)^2`
`Q=10000`
Vậy tại `x=-10;y=-10` thì `Q=10000`
\(a)P=x\left(x^2-y\right)+y\left(x-y^2\right)\\ =x^3-xy+xy-y^3\\ =x^3-y^3\)
Thay `x=-1/2` và `y=-1/2` vào P ta có:
\(P=\left(-\dfrac{1}{2}\right)^3-\left(-\dfrac{1}{2}\right)^3=0\)
\(b)Q=x^2\left(y^3-xy^2\right)+\left(-y+x+1\right)x^2y^2\\ =x^2y^3-x^3y^2-x^2y^3+x^3y^2+x^2y^2\\ =x^2y^2\)
Thay `x=-10` và `y=-10` vào Q ta có:
\(Q=\left(-10\right)^2\cdot\left(-10\right)^2=100\cdot100=10000\)