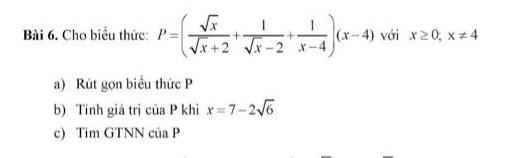a) \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{x-4}\right)\left(x-4\right)\)
\(=\left[\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right]\left(x-4\right)\)
\(=\left[\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right]\left(x-4\right)\)
\(=\dfrac{x-2\sqrt{x}+\sqrt{x}+2+1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\left(x-4\right)\)
\(=\dfrac{x-\sqrt{x}+3}{x-4}\cdot\left(x-4\right)\)
\(=x-\sqrt{x}+3\)
b) \(x=7-2\sqrt{6}=\left(\sqrt{6}\right)^2-2\cdot\sqrt{6}\cdot1+1^2=\left(\sqrt{6}-1\right)^2\)
Thay vào P ta có:
\(P=\left(7-2\sqrt{6}\right)-\sqrt{\left(\sqrt{6}-1\right)^2}+3=7-2\sqrt{6}-\sqrt{6}+1+3\)
\(=11-3\sqrt{6}\)
c) \(P=x-\sqrt{x}+3=x-2\cdot\sqrt{x}\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\dfrac{11}{4}\)
\(=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\forall x\ge0\)
Dấu "=" xảy ra khi: \(\sqrt{x}-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{4}\left(tm\right)\)
Vậy: ...
a) Với $x\ge0;x\ne4$, ta có:
\(P=\left(\frac{\sqrt x}{\sqrt x+2}+\frac{1}{\sqrt x-2}+\frac{1}{x-4}\right)(x-4)\\=\left[\frac{\sqrt x(\sqrt x-2)}{(\sqrt x-2)(\sqrt x+2)}+\frac{\sqrt x+2}{(\sqrt x-2)(\sqrt x+2)}+\frac{1}{(\sqrt x-2)(\sqrt x+2)}\right](x-4)\\= \frac{x-2\sqrt x+\sqrt x+2+1}{(\sqrt x-2)(\sqrt x+2)}.(\sqrt x-2)(\sqrt x+2)\\=x-\sqrt x+3\)
b) Với \(x=7-2\sqrt 6\), thay vào P ta được:
\(P=7-2\sqrt 6-\sqrt{7-2\sqrt6 }+3\\=10-2\sqrt6-\sqrt{(\sqrt6)^2-2.\sqrt6.1+1^2}\\=10-2\sqrt6-\sqrt{(\sqrt6-1)^2}\\=10-2\sqrt6-|\sqrt6 -1|\\=10-2\sqrt6 -(\sqrt 6-1)(\text{vì }\sqrt 6>1)\\=11-3\sqrt 6\)
c) Ta có:
\(P=x-\sqrt x+3\\=\left[(\sqrt x)^2-2.\sqrt x.\frac12+\left(\frac12\right)^2\right]-\frac14+3\\=\left(\sqrt x-\frac12\right)^2+\frac{11}{4}\)
Ta thấy:
\(\left(\sqrt x-\frac12\right)^2\ge 0\forall x\ge 0\\\Rightarrow \left(\sqrt x-\frac12\right)^2+\frac{11}{4}\ge \frac{11}{4}\forall x\ge 0\\\Rightarrow P\ge\frac{11}{4}\)
Dấu "=" xảy ra khi: \(\sqrt x-\frac12=0\Leftrightarrow \sqrt x=\frac12\)
\(\Rightarrow x=\frac14\) (tm ĐKXĐ)
Vậy \(P_{min}=\frac{11}{4}\) tại \(x=\frac14\).
$\text{#}Toru$