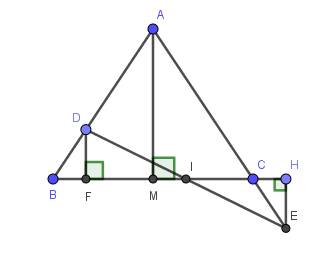
a) Do \(\Delta ABC\) cân tại A (gt)
\(\Rightarrow AB=AC\) và \(\widehat{ABC}=\widehat{ACB}\)
Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\left(cmt\right)\)
\(AM\) là cạnh chung
\(\Rightarrow\Delta ABM=\Delta ACM\) (hai cạnh góc vuông)
\(\Rightarrow MB=MC\) (hai cạnh tương ứng)
b) Do \(EH\perp BC\left(gt\right)\)
\(\Rightarrow\Delta CHE\) vuông tại H
\(\Rightarrow\widehat{CEH}+\widehat{HCE}=90^0\)
Mà \(\widehat{HCE}=\widehat{ACB}\) (đối đỉnh)
\(\Rightarrow\widehat{CEH}+\widehat{ACB}=90^0\)
Mà \(\widehat{ACB}=\widehat{ABC}\left(cmt\right)\)
\(\Rightarrow\widehat{CEH}+\widehat{ABC}=90^0\) (1)
Do \(DF\perp BC\left(gt\right)\)
\(\Rightarrow\Delta BDF\) vuông tại F
\(\Rightarrow\widehat{BDF}+\widehat{DBF}=90^0\)
\(\Rightarrow\widehat{BDF}+\widehat{ABC}=90^0\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{BDF}=\widehat{CEH}\)
Xét hai tam giác vuông: \(\Delta BDF\) và \(\Delta CEH\) có:
\(BD=CE\left(gt\right)\)
\(\widehat{BDF}=\widehat{CEH}\left(cmt\right)\)
\(\Rightarrow\Delta BDF=\Delta CEH\) (cạnh huyền - góc nhọn)
\(\Rightarrow DF=EH\) (hai cạnh tương ứng)
Do \(DF\perp BC\left(gt\right)\)
\(EH\perp BC\left(gt\right)\)
\(\Rightarrow DF\) // \(EH\)
\(\Rightarrow\widehat{FDI}=\widehat{HEI}\) (so le trong)
Xét hai tam giác vuông: \(\Delta FDI\) và \(\Delta HEI\) có:
\(DF=EH\left(cmt\right)\)
\(\widehat{FDI}=\widehat{HEI}\left(cmt\right)\)
\(\Rightarrow\Delta FDI=\Delta HEI\) (cạnh góc vuông - góc nhọn kề)
\(\Rightarrow DI=EI\) (hai cạnh tương ứng)
\(\Rightarrow I\) là trung điểm của DE
a: Xét ΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
Do đó: ΔABM=ΔACM
=>MB=MC
b: Xét ΔDFB vuông tại F và ΔEHC vuông tại H có
DB=EC
\(\widehat{DBF}=\widehat{ECH}\left(=\widehat{ACB}\right)\)
Do đó: ΔDFB=ΔEHC
=>DF=EH
Xét ΔIFD vuông tại F và ΔIHE vuông tại H có
FD=HE
\(\widehat{IDF}=\widehat{IEH}\)(DF//EH)
Do đó: ΔIFD=ΔIHE
=>ID=IE
=>I là trung điểm của DE
















