`*` Bài 2.
Gọi `x` là chiều dài của mảnh vườn đó
`y` là chiều rộng của mảnh vườn đó
`(m;x,y>0)`
`-` Vì mảnh vườn hình chữ nhật có chu vi `56m` nên:
`(x+y)*2=56` `=>2x+2y=56` `(1)`
`-` Vì nếu tăng chiều dài `4m` và giảm chiều rộng `2m` thì diện tích tăng `8m^2` nên:
`(x+4)(y-2)=xy-8`
`=> xy -2x +4y - 8 =xy-8`
`=> xy -2x+4y-xy = -8+8`
`=> -2x+4y=0` `(2)`
Từ `(1)` và `(2)`, ta có hệ phương trình: \(\left\{{}\begin{matrix}2x+2y=56\\-2x+4y=0\end{matrix}\right.\)
Giải hệ phương trình, ta được: \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{56}{3}\\y=\dfrac{28}{3}\end{matrix}\right.\left(nhận\right)\)
Vậy, chiều dài của mảnh vườn đó là `56/3 m`.
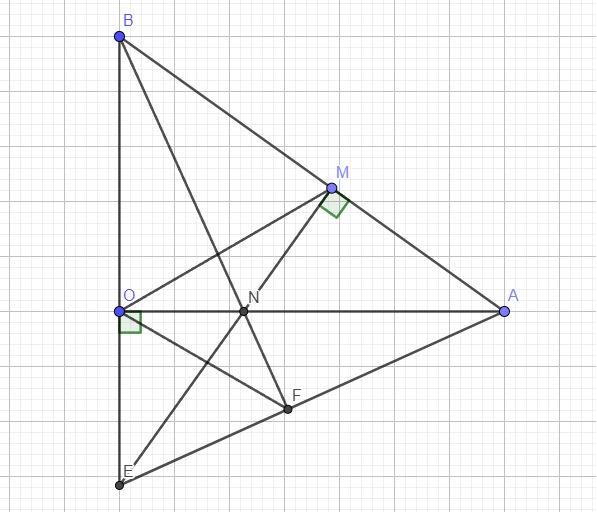
a.
Do \(EM\perp AB\left(gt\right)\Rightarrow\widehat{EMB}=90^0\)
Xét hai tam giác OAB và và MEB có:
\(\left\{{}\begin{matrix}\widehat{EBM}-chung\\\widehat{AOB}=\widehat{EMB}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta OAB\sim\Delta MEB\left(g.g\right)\)
b.
Xét hai tam giác AMN và AOB có:
\(\left\{{}\begin{matrix}\widehat{MAN}-chung\\\widehat{AMN}=\widehat{AOB}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta AMN\sim\Delta AOB\left(g.g\right)\)
\(\Rightarrow\dfrac{AM}{AO}=\dfrac{AN}{AB}\Rightarrow AN.AO=AM.AB\)
c.
Từ \(AN.AO=AM.AB\Rightarrow\dfrac{AO}{AB}=\dfrac{AM}{AN}\)
Xét hai tam giác AMO và ANB có:
\(\left\{{}\begin{matrix}\dfrac{AO}{AB}=\dfrac{AM}{AN}\\\widehat{MAO}-chung\end{matrix}\right.\)
\(\Rightarrow\Delta AMO\sim\Delta ANB\left(c.g.c\right)\)
\(\Rightarrow\widehat{AOM}=\widehat{NBA}\) (1)
Trong tam giác ABE, có \(AO\perp BE\) ; \(EM\perp AB\), mà AO và EM cắt nhau tại N
\(\Rightarrow N\) là trực tâm tam giác ABE \(\Rightarrow BN\) là đường cao thứ 3
\(\Rightarrow BN\perp AE\) tại F hay \(\widehat{NFA}=90^0\)
Xét hai tam giác NFA và NOB có:
\(\left\{{}\begin{matrix}\widehat{NFA}=\widehat{NOB}=90^0\\\widehat{FNA}=\widehat{ONB}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta NFA\sim\Delta NOB\left(g.g\right)\Rightarrow\dfrac{NF}{NO}=\dfrac{NA}{NB}\Rightarrow\dfrac{NF}{NA}=\dfrac{NO}{NB}\)
Xét hai tam giác NFO và NAB có:
\(\left\{{}\begin{matrix}\dfrac{NF}{NA}=\dfrac{NO}{NB}\left(cmt\right)\\\widehat{ONF}=\widehat{BNA}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta NFO\sim\Delta NAB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NOF}=\widehat{NBA}\) (2)
(1);(2) \(\Rightarrow\widehat{NOF}=\widehat{AOM}\) \(\Rightarrow OA\) là phân giác \(\widehat{FOM}\)
4.
\(a^2+b^2+c^2=\left(a+b+c\right)^2\)
\(\Leftrightarrow a^2+b^2+c^2=a^2+b^2+c^2+2\left(ab+bc+ca\right)\)
\(\Leftrightarrow ab+bc+ca=0\)
\(\Rightarrow\left\{{}\begin{matrix}ab=-\left(bc+ca\right)\\bc=-\left(ab+ca\right)\\ca=-\left(ab+bc\right)\end{matrix}\right.\)
Thay vào:
\(\dfrac{a^2}{a^2+2bc}+\dfrac{b^2}{b^2+2ca}+\dfrac{c^2}{c^2+2ab}=\dfrac{a^2}{a^2+bc+bc}+\dfrac{b^2}{b^2+ca+ca}+\dfrac{c^2}{c^2+ab+ab}\)
\(=\dfrac{a^2}{a^2+bc-\left(ab+ca\right)}+\dfrac{b^2}{b^2+ca-\left(ab+bc\right)}+\dfrac{c^2}{c^2+ab-\left(bc+ca\right)}\)
\(=\dfrac{a^2}{a\left(a-b\right)-c\left(a-b\right)}+\dfrac{b^2}{b\left(b-c\right)-a\left(b-c\right)}+\dfrac{c^2}{b\left(a-c\right)-c\left(a-c\right)}\)
\(=\dfrac{a^2}{\left(a-b\right)\left(a-c\right)}-\dfrac{b^2}{\left(a-b\right)\left(b-c\right)}+\dfrac{c^2}{\left(a-c\right)\left(b-c\right)}\)
\(=\dfrac{a^2\left(b-c\right)-b^2\left(a-c\right)+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{a^2b-a^2c-ab^2+b^2c+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{ab\left(a-b\right)-c\left(a^2-b^2\right)+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{ab\left(a-b\right)-c\left(a+b\right)\left(a-b\right)+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{\left(a-b\right)\left(ab-ac-bc+c^2\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=\dfrac{\left(a-b\right)\left[a\left(b-c\right)-c\left(b-c\right)\right]}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=1\)