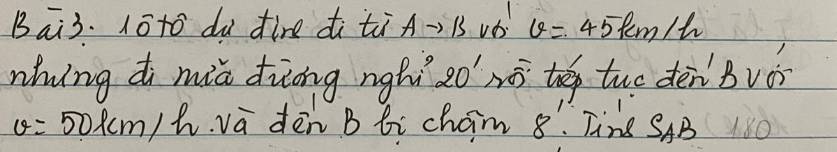Lời giải:
Đổi 8 phút = $\frac{2}{15}$ giờ
Thời gian dự định đi từ A đến B của ô tô:
$\frac{AB}{45}$ (giờ)
Nửa đường ô tô đi với: $\frac{AB}{2.45}=\frac{AB}{90}$ (giờ)
Ô tô nghỉ giữa đường 20p, tức là nghỉ $\frac{1}{3}$ giờ
Ô tô đi tiếp nửa quãng đường với vận tốc 50 km/h, hết $\frac{AB}{2.50}=\frac{AB}{100}$ (giờ)
Theo bài ra ta có:
$\frac{AB}{45}+\frac{2}{15}=\frac{AB}{90}+\frac{1}{3}+\frac{AB}{100}$
$\Leftrightarrow \frac{2}{15}-\frac{1}{3}=\frac{AB}{90}+\frac{AB}{100}-\frac{AB}{45}$
$\Leftrightarrow \frac{-1}{5}=\frac{AB}{-900}$
$\Rightarrow AB=180$ (km)
Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian dự định đi hết quãng đường là \(\dfrac{x}{45}\left(giờ\right)\)
Thời gian đi nửa quãng đường đầu tiên là;
\(\dfrac{x}{2}:45=\dfrac{x}{90}\left(giờ\right)\)
Thời gian đi nửa quãng đường còn lại là: \(\dfrac{x}{2}:50=\dfrac{x}{100}\left(giờ\right)\)
Tổng thời gian đi thực tế là \(\dfrac{x}{90}+\dfrac{x}{100}+\dfrac{1}{3}\left(giờ\right)\)
Ô tô đến B chậm 8p=2/15 giờ nên ta có phương trình:
\(\dfrac{x}{90}+\dfrac{x}{100}+\dfrac{1}{3}-\dfrac{x}{45}=\dfrac{2}{15}\)
=>\(\dfrac{10x+9x-20x}{900}=\dfrac{2}{15}-\dfrac{1}{3}=\dfrac{2}{15}-\dfrac{5}{15}=-\dfrac{3}{15}=-\dfrac{1}{5}\)
=>\(-\dfrac{x}{900}=-\dfrac{1}{5}\)
=>x=180(nhận)
Vậy: Độ dài quãng đường AB là 180km