Bài 1:
a) \(5x-11=4\)
\(\Leftrightarrow5x=4+11\)
\(\Leftrightarrow5x=15\)
\(\Leftrightarrow x=15:5=3\)
Vậy: ...
b) \(7x+12=-2\)
\(\Leftrightarrow7x=-2-12\)
\(\Leftrightarrow7x=-14\)
\(\Leftrightarrow x=-14:7=-2\)
Vậy: ...
c) \(17-8x=5-6x\)
\(\Leftrightarrow-6x+8x=17-5\)
\(\Leftrightarrow2x=12\)
\(\Leftrightarrow x=12:2=6\)
Vậy: ...
d) \(3x\left(x-3\right)-\left(x^2-9\right)=0\)
\(\Leftrightarrow3x\left(x-3\right)-\left(x+3\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x-x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\2x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy: ...
Bài 2
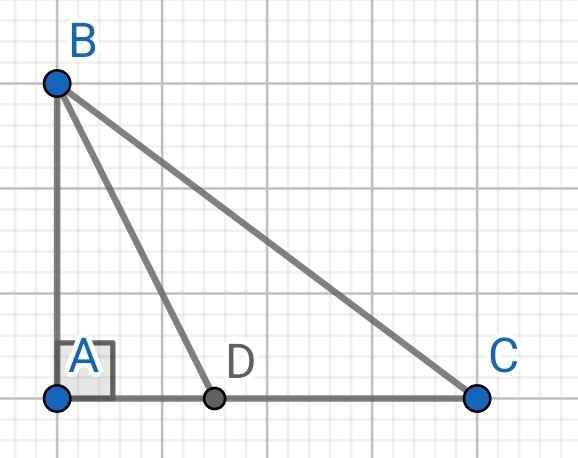
∆ABC vuông tại A (gt)
⇒ BC² = AB² + AC² (Pythagore)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
∆ABC có BD là đường phân giác (gt)
⇒ DA/DC = AB/BC
⇒ DA/AB = DC/BC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
DA/AB = DC/BC = (DA + DC)/(AB + BC) = 8/16 = 1/2
DA/AB = 1/2 ⇒ DA = AB . 1/2 = 6 . 1/2 = (cm)
DC/BC = 1/2 ⇒ DC = BC . 1/2 = 10 . 1/2 = 5 (cm)
Vậy DA = 3 cm, DC = 5 cm
Bài 3
Do ∆ABC ∽ ∆DEF (gt)
⇒ AB/DE = AC/DF = BC/EF = 18/12 = 3/2
AB/DE = 3/2 ⇒ AB = DE . 3/2 = 6 . 3/2 = 9
AC/DF = 3/2 ⇒ AC = DF . 3/2 = 10 . 3/2 = 15
Bài 1
a) 5x - 11 = 4
5x = 4 + 11
5x = 15
x = 15 : 5
x = 3
Vậy S = {3}
b) 7x + 12 = -2
7x = -2 - 12
7x = -14
x = -14 : 7
x = -2
Vậy S = {-2}
c) 17 - 8x = 5 - 6x
-8x + 6x = 5 - 17
-2x = -12
x = -12 : (-2)
x = 6
Vậy S = {6}
d) 3x(x - 3) - (x² - 9) = 0
3x(x - 3) - (x - 3)(x + 3) = 0
(x - 3)[3x - (x + 3)] = 0
(x - 3)(3x - x - 3) = 0
(x - 3)(2x - 3) = 0
x - 3 = 0 hoặc 2x - 3 = 0
*) x - 3 = 0
x = 3
*) 2x - 3 = 0
2x = 3
x = 3/2
Vậy S = {3/2; 3}
Bài 1
e) (x + 4)(3x + 5) - (x² - 16) = 0
(x + 4)(3x + 5) - (x - 4)(x + 4) = 0
(x + 4)[3x + 5 - (x - 4)] = 0
(x + 4)(3x + 5 - x + 4) = 0
(x + 4)(2x + 9) = 0
x + 4 = 0 hoặc 2x + 9 = 0
*) x + 4 = 0
x = -4
*) 2x + 9 = 0
2x = -9
x = -9/2
Vậy S = {-9/2; -4}
f) (x - 3)(3 - 4x) + (x² - 6x + 9) = 0
(x - 3)(3 - 4x) + (x - 3)² = 0
(x - 3)(3 - 4x + x - 3) = 0
(x - 3).(-3x) = 0
-3x = 0 hoặc x - 3 = 0
*) -3x = 0
x = 0
*) x - 3 = 0
x = 3
Vậy S = {0; 3}
g) Phương trình đã cho tương đương:
3(2x - 10) = 12.5 + 2(2 - 3x)
6x - 30 = 60 + 4 - 6x
6x + 6x = 64 + 30
12x = 94
x = 48/7
Vậy S = {48/7}
Bài 1
h) (x - 1)³ + (x + 2)³ = (2x + 1)³
x³ - 3x² + 3x - 1 + x³ + 6x² + 12x + 8 = 8x³ + 12x² + 6x + 1
2x³ + 3x² + 15x + 7 - 8x³ - 12x² - 6x - 1 = 0
-6x³ - 9x² + 9x + 6 = 0
(-6x³ + 6) + (-9x² + 9x) = 0
-6(x³ - 1) - 9x(x - 1) = 0
-6(x - 1)(x² + x + 1) - 9x(x - 1) = 0
(x - 1)[-6(x² + x + 1) - 9x] = 0
(x - 1)(-6x² - 6x - 6 - 9x) = 0
(x - 1)(-6x² - 15x - 6) = 0
-3(x - 1)(2x² + 5x + 2) = 0
x - 1 = 0 hoặc 2x² + 5x + 2 = 0
*) x - 1 = 0
x = 1
*) 2x² + 5x + 2 = 0
2x² + 4x + x + 2 = 0
(2x² + 4x) + (x + 2) = 0
2x(x + 2) + (x + 2) = 0
(x + 2)(2x + 1) = 0
x + 2 = 0 hoặc 2x + 1 = 0
+) x + 2 = 0
x = -2
+) 2x + 1 = 0
2x = -1
x = -1/2
Vậy S = {-2; -1/2; 1}
Bài 1
k) (x² - 5x - 2018)/2024 + (x² - 5x - 2015)/2021 = (x² - 5x - 2017)/2023 + (x² - 5x - 2016)/2022
[(x² - 5x + 6) - 2024]/2024 + [(x² - 5x + 6) - 2021]/2021 = [(x² - 5x + 6) - 2023]/2023 + [(x² - 5x + 6) - 2022]/2022
(x² - 5x + 6)/2024 - 1 + (x² - 5x + 6)/2021 - 1 = (x² - 5x + 6)/2023 - 1 + (x² - 5x + 6)/2022 - 1
(x² - 5x + 6)/2024 + (x² - 5x + 6)/2021 - (x² - 5x + 6)/2023 - (x² - 5x + 6)/2022 = 0
(x² - 5x + 6)/(1/2024 + 1/2021 - 1/2023 - 1/2022) = 0
x² - 5x + 6 = 0
x² - 2x - 3x + 6 = 0
(x² - 2x) - (3x - 6) = 0
x(x - 2) - 3(x - 2) = 0
(x - 2)(x - 3) = 0
x - 2 = 0 hoặc x - 3 = 0
*) x - 2 = 0
x = 2
*) x - 3 = 0
x = 3
Vậy S = {2; 3}


















