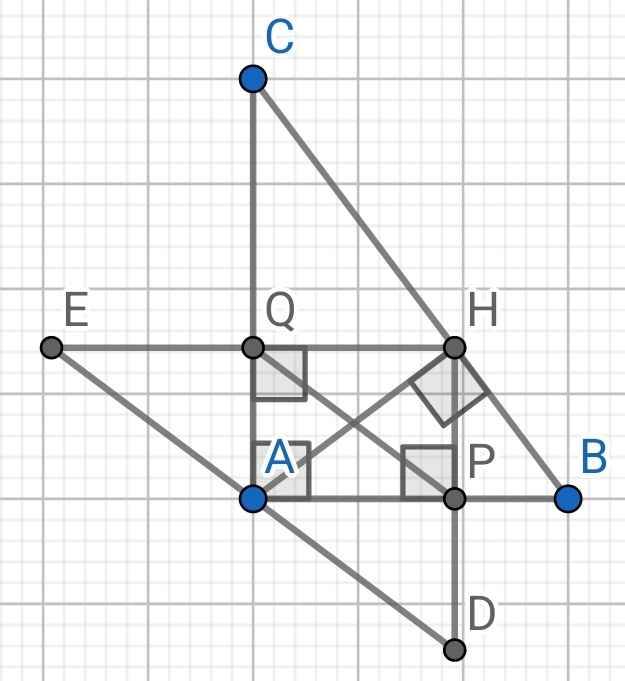
a) Do QH = QE (gt)
⇒ Q là trung điểm của HE
Mà AQ ⊥ HE (gt)
⇒ AQ vừa là đường trung tuyến, vừa là đường cao của ∆AHE
∆AHE cân tại A
⇒ AQ là đường phân giác của ∆HAE
⇒ ∠HAQ = ∠EAQ (1)
Do AB ⊥ AC (∆ABC vuông tại A)
⇒ AQ ⊥ AP
⇒ ∠HAQ + ∠HAP = 90⁰ (2)
Do PH = PD (gt)
⇒ P là trung điểm của HD
⇒ AP là đường trung tuyến của ∆AHD
∆AHD có:
AP là đường trung tuyến
AP là đường cao (AP ⊥ HD)
⇒ ∆AHD cân tại A
⇒ AP là đường phân giác của ∆AHD
⇒ ∠HAP = ∠DAP (3)
Từ (1), (2) và (3) ⇒ ∠EAQ + ∠DAP = 90⁰
⇒ E, A, D thẳng hàng (*)
Do ∆AHE cân tại A (cmt)
⇒ AH = AE (4)
Do ∆AHD cân tại A (cmt)
⇒ AH = AD (5)
Từ (4) và (5) ⇒ AD = AE (**)
Từ (*) và (**) ⇒ A là trung điểm của DE
b) ∆DEH có:
P là trung điểm của HD (cmt)
Q là trung điểm của HE (cmt)
⇒ PQ là đường trung bình của ∆DEH
⇒ PQ = DE : 2
c) Tứ giác APHQ có:
∠AQH = ∠APH = ∠PAQ = 90⁰
⇒ APHQ là hình chữ nhật
⇒ PQ = AH (hai đường chéo của hình chữ nhật)

a) Do QH = QE (gt)
⇒ Q là trung điểm của HE
Mà AQ ⊥ HE (gt)
⇒ AQ vừa là đường trung tuyến, vừa là đường cao của ∆AHE
∆AHE cân tại A
⇒ AQ là đường phân giác của ∆HAE
⇒ ∠HAQ = ∠EAQ (1)
Do AB ⊥ AC (∆ABC vuông tại A)
⇒ AQ ⊥ AP
⇒ ∠HAQ + ∠HAP = 90⁰ (2)
Do PH = PD (gt)
⇒ P là trung điểm của HD
⇒ AP là đường trung tuyến của ∆AHD
∆AHD có:
AP là đường trung tuyến
AP là đường cao (AP ⊥ HD)
⇒ ∆AHD cân tại A
⇒ AP là đường phân giác của ∆AHD
⇒ ∠HAP = ∠DAP (3)
Từ (1), (2) và (3) ⇒ ∠EAQ + ∠DAP = 90⁰
⇒ E, A, D thẳng hàng (*)
Do ∆AHE cân tại A (cmt)
⇒ AH = AE (4)
Do ∆AHD cân tại A (cmt)
⇒ AH = AD (5)
Từ (4) và (5) ⇒ AD = AE (**)
Từ (*) và (**) ⇒ A là trung điểm của DE
b) ∆DEH có:
P là trung điểm của HD (cmt)
Q là trung điểm của HE (cmt)
⇒ PQ là đường trung bình của ∆DEH
⇒ PQ = DE : 2
c) Tứ giác APHQ có:
∠AQH = ∠APH = ∠PAQ = 90⁰
⇒ APHQ là hình chữ nhật
⇒ PQ = AH (hai đường chéo của hình chữ nhật)
















