Question

  

Answer 1

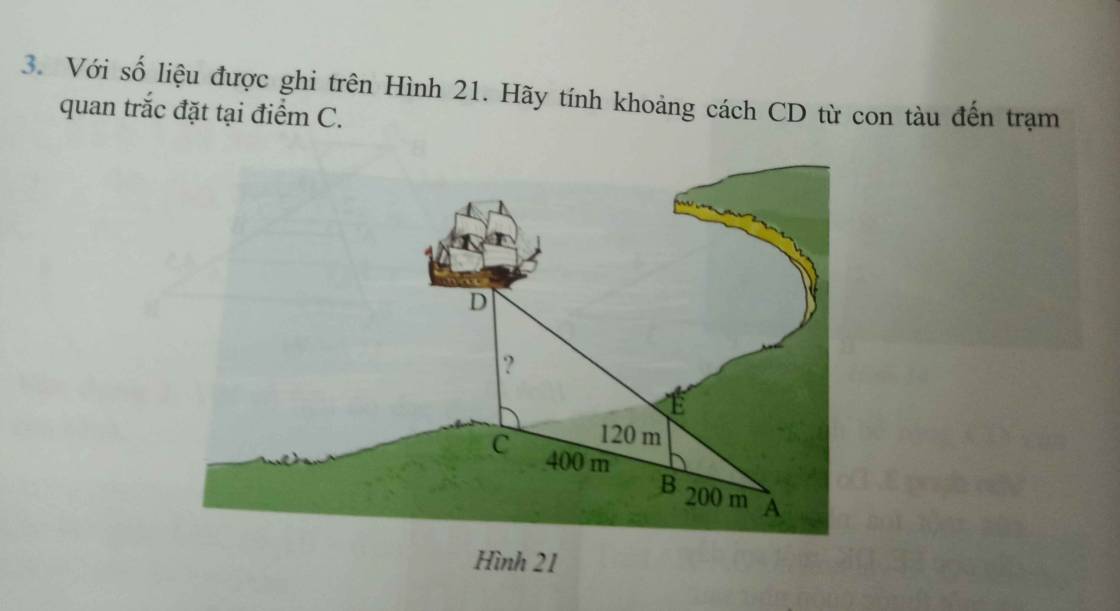
Ta có: \(\widehat{EBA}=\widehat{DCA}\)

mà hai góc này là hai góc ở vị đồng vị

nên EB//DC

ta có: AB+BC=AC

=>AC=200+400=600(m)

Xét ΔADC có EB//DC

nên \(\dfrac{EB}{DC}=\dfrac{AB}{AC}\)

=>\(\dfrac{120}{DC}=\dfrac{200}{600}=\dfrac{1}{3}\)

=>\(DC=120\cdot3=360\)(m)

Answer 2

Do \(\widehat{BCD}=\widehat{ABE}\), mà chúng là 2 góc đồng vị \(\Rightarrow BE||CD\)

Áp dụng định lý Thales:

\(\dfrac{BE}{CD}=\dfrac{AB}{AC}=\dfrac{AB}{AB+BC}\Rightarrow CD=\dfrac{BE\left(AB+CA\right)}{AB}=\dfrac{120.\left(400+200\right)}{200}=360\left(m\right)\)