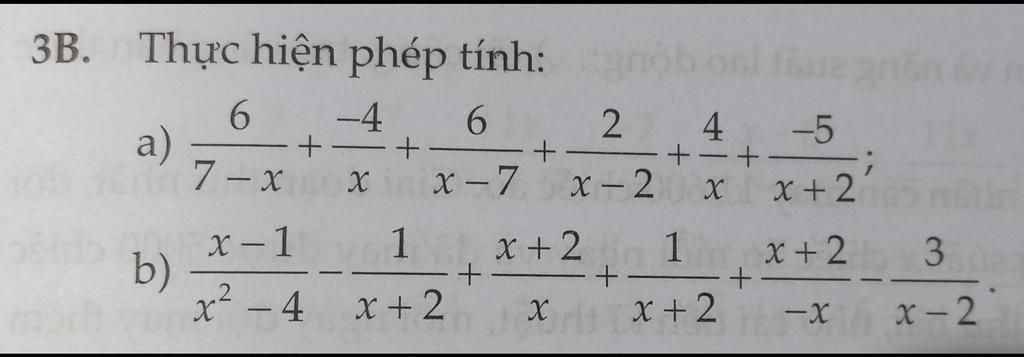a: ĐKXĐ: \(x\notin\left\{7;0;2;-2\right\}\)
\(\dfrac{6}{7-x}+\dfrac{-4}{x}+\dfrac{6}{x-7}+\dfrac{2}{x-2}+\dfrac{4}{x}+\dfrac{-5}{x+2}\)
\(=\left(\dfrac{6}{x-7}-\dfrac{6}{x-7}\right)+\left(-\dfrac{4}{x}+\dfrac{4}{x}\right)+\dfrac{2}{x-2}-\dfrac{5}{x+2}\)
\(=\dfrac{2}{x-2}-\dfrac{5}{x+2}\)
\(=\dfrac{2x+4-5x+10}{\left(x-2\right)\left(x+2\right)}=\dfrac{-3x+14}{\left(x-2\right)\left(x+2\right)}\)
b: ĐKXĐ: \(x\notin\left\{0;2;-2\right\}\)
\(\dfrac{x-1}{x^2-4}-\dfrac{1}{x+2}+\dfrac{x+2}{x}+\dfrac{1}{x+2}+\dfrac{x+2}{-x}-\dfrac{3}{x-2}\)
\(=\left(-\dfrac{1}{x+2}+\dfrac{1}{x+2}\right)+\left(\dfrac{x+2}{x}-\dfrac{x+2}{x}\right)+\dfrac{x-1}{\left(x-2\right)\left(x+2\right)}-\dfrac{3}{x-2}\)
\(=\dfrac{x-1}{\left(x-2\right)\left(x+2\right)}-\dfrac{3}{x-2}\)
\(=\dfrac{x-1-3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{x-1-3x-6}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{-2x-7}{\left(x-2\right)\left(x+2\right)}\)
\(a,\dfrac{6}{7-x}+\dfrac{-4}{x}+\dfrac{6}{x-7}+\dfrac{2}{x-2}+\dfrac{4}{x}+\dfrac{-5}{x+2}\\ =-\dfrac{6}{x-7}-\dfrac{4}{x}+\dfrac{6}{x-7}+\dfrac{2}{x-2}+\dfrac{4}{x}-\dfrac{5}{x+2}\\ =\left(\dfrac{6}{x-7}-\dfrac{6}{x-7}\right)+\left(\dfrac{4}{x}-\dfrac{4}{x}\right)-\left(\dfrac{5}{x+2}-\dfrac{2}{x-2}\right)\\ =0+0-\dfrac{3}{x-2}=\dfrac{-3}{x-2}\\ ---\\ b,\dfrac{x-1}{x^2-4}-\dfrac{1}{x+2}+\dfrac{x+2}{x}+\dfrac{1}{x+2}+\dfrac{x+2}{-x}-\dfrac{3}{x-2}\\ =\dfrac{x-1}{x^2-4}+\left(\dfrac{1}{x+2}-\dfrac{1}{x+2}\right)+\left(\dfrac{x+2}{x}-\dfrac{x+2}{x}\right)-\dfrac{3}{x-2}\\ =\dfrac{x-1}{\left(x-2\right)\left(x+2\right)}+0+0-\dfrac{3}{x-2}\\ =\dfrac{\left(x-1\right)-3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{-2x-7}{\left(x-2\right)\left(x+2\right)}=-\dfrac{2x+7}{x^2-4}\)