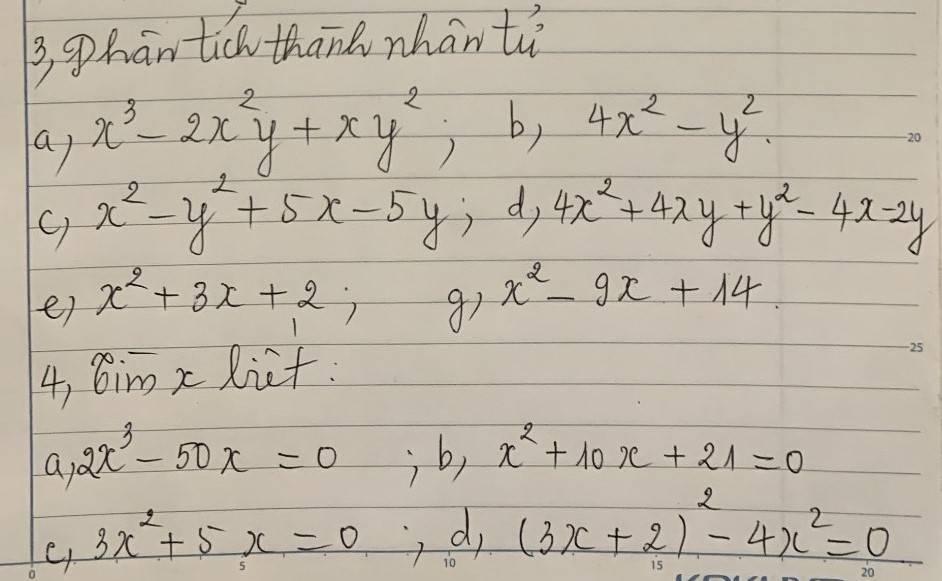3,
a) \(x^3-2x^2y+xy^2\)
\(=x\left(x^2-2xy+y^2\right)\)
\(=x\left(x-y\right)^2\)
b) \(4x^2-y^2\)
\(=\left(2x\right)^2-y^2\)
\(=\left(2x-y\right)\left(2x+y\right)\)
c) \(x^2-y^2+5x-5y\)
\(=\left(x^2-y^2\right)+\left(5x-5y\right)\)
\(=\left(x-y\right)\left(x+y\right)+5\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y+5\right)\)
d) \(4x^2+4xy+y^2-4x-2y\)
\(=\left(4x^2+4xy+y^2\right)-\left(4x+2y\right)\)
\(=\left[\left(2x\right)^2+2\cdot2x\cdot y+y^2\right]-2\left(2x+y\right)\)
\(=\left(2x+y\right)^2-2\left(2x+y\right)\)
\(=\left(2x+y\right)\left(2x+y-2\right)\)
e) \(x^2+3x+2\)
\(=x^2+x+2x+2\)
\(=x\left(x+1\right)+2\left(x+1\right)\)
\(=\left(x+1\right)\left(x+2\right)\)
g) \(x^2-9x+14\)
\(=x^2-2x-7x+14\)
\(=x\left(x-2\right)-7\left(x-2\right)\)
\(=\left(x-2\right)\left(x-7\right)\)
4,
a) \(2x^3-50x=0\)
\(\Rightarrow2x\left(x^2-25\right)=0\)
\(\Rightarrow2x\left(x-5\right)\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x-5=0\\x+5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)
b) \(x^2+10x+21=0\)
\(\Rightarrow x^2+3x+7x+21=0\)
\(\Rightarrow x\left(x+3\right)+7\left(x+3\right)=0\)
\(\Rightarrow\left(x+3\right)\left(x+7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+3=0\\x+7=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-3\\x=-7\end{matrix}\right.\)
c) \(3x^2+5x=0\)
\(\Rightarrow x\left(3x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\3x+5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{3}\end{matrix}\right.\)
d) \(\left(3x+2\right)^2-4x^2=0\)
\(\Rightarrow\left(3x+2\right)^2-\left(2x\right)^2=0\)
\(\Rightarrow\left(3x+2-2x\right)\left(3x+2+2x\right)=0\)
\(\Rightarrow\left(x+2\right)\left(5x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\5x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=-\dfrac{2}{5}\end{matrix}\right.\)
\(\text{#}Toru\)
4:
a: \(2x^3-50x=0\)
=>\(2\left(x^3-25x\right)=0\)
=>\(x^3-25x=0\)
=>\(x\left(x^2-25\right)=0\)
=>\(x\left(x-5\right)\left(x+5\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x-5=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\\x=5\end{matrix}\right.\)
b: \(x^2+10x+21=0\)
=>\(x^2+3x+7x+21=0\)
=>\(\left(x^2+3x\right)+\left(7x+21\right)=0\)
=>\(x\left(x+3\right)+7\cdot\left(x+3\right)=0\)
=>(x+3)(x+7)=0
=>\(\left[{}\begin{matrix}x+3=0\\x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-7\end{matrix}\right.\)
c: \(3x^2+5x=0\)
=>\(x\left(3x+5\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\3x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{3}\end{matrix}\right.\)
d: \(\left(3x+2\right)^2-4x^2=0\)
=>\(\left(3x+2\right)^2-\left(2x\right)^2=0\)
=>(3x+2+2x)(3x+2-2x)=0
=>(x+2)(5x+2)=0
=>\(\left[{}\begin{matrix}x+2=0\\5x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-\dfrac{2}{5}\end{matrix}\right.\)