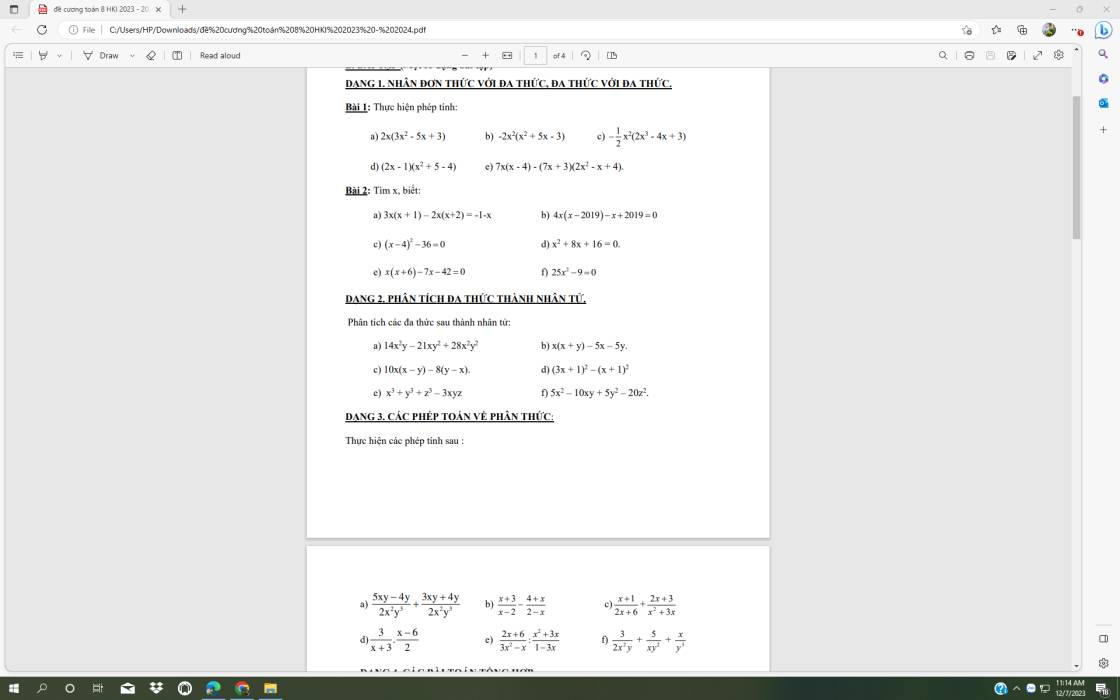
Bài 1
a) 2x(3x² - 5x + 3)
= 2x.3x² - 2x.5x + 2x.3
= 6x³ - 10x² + 6x
b) -2x²(x² + 5x - 3)
= -2x².x² - 2x².5x + 2x².3
= 2x⁴ - 10x³ + 6x²
c) -1/2 x²(2x³ - 4x + 3)
= -1/2 x².2x³ + 1/2 x².4x - 1/2 x².3
= -x⁵ + 2x³ - 3/2 x²
d) (2x - 1)(x² + 5x - 4)
= 2x.x² + 2x.5x - 2x.4 - 1.x² - 1.5x + 1.4
= 2x³ + 10x² - 8x - x² - 5x + 4
= 2x³ - 9x² - 13x + 4
e) 7x(x - 4) - (7x + 3)(2x² - x + 4)
= 7x.x - 7x.4 - 7x.2x² + 7x.x - 7x.4 - 3.2x² + 3.x - 3.4
= 7x² - 28x - 14x³ + 7x² - 28x - 6x² + 3x - 12
= -14x³ + 8x² - 53x - 12
Bài 2
a) 3x(x + 1) - 2x(x + 2) = -1 - x
3x² + 3x - 2x² - 4x = -1 - x
x² + 3x - 4x + x = -1
x² = -1 (vô lý)
Vậy không tìm được x thỏa mãn đề bài
b) 4x(x - 2019) - x + 2019 = 0
4x(x - 2019) - (x - 2019) = 0
(x - 2018)(4x - 1) = 0
x - 2018 = 0 hoặc 4x - 1 = 0
*) x - 2018 = 0
x = 2018
*) 4x - 1 = 0
4x = 1
x = 1/4
Vậy x = 1/4; x = 2018
c) (x - 4)² - 36 = 0
(x - 4)² - 6² = 0
(x - 4 - 6)(x - 4 + 6) = 0
(x - 10)(x + 2) = 0
x - 10 = 0 hoặc x + 2 = 0
*) x - 10 = 0
x = 10
*) x + 2 = 0
x = -2
Vậy x = -2; x = 10
d) x² + 8x + 16 = 0
x² + 2.x.4 + 4² = 0
(x + 4)² = 0
x + 4 = 0
x = -4
e) x(x + 6) - 7x - 42 = 0
x(x + 6) - (7x + 42) = 0
x(x + 6) - 7(x + 6) = 0
(x + 6)(x - 7) = 0
x + 6 = 0 hoặc x - 7 = 0
*) x + 6 = 0
x = -6
*) x - 7 = 0
x = 7
Vậy x = -6; x = 7
f) 25x² - 9 = 0
(5x)² - 3² = 0
(5x - 3)(5x + 3) = 0
5x - 3 = 0 hoặc 5x + 3 = 0
*) 5x - 3 = 0
5x = 3
x = 3/5
*) 5x + 3 = 0
5x = -3
x = -3/5
Vậy x = -3/5; x = 3/5
DẠNG 2
a) 14x²y - 21xy² + 28x²y²
= 7xy(2x - 3y + 4xy)
b) x(x + y) - 5x - 5y
= x(x + y) - (5x + 5y)
= x(x + y) - 5(x + y)
= (x + y)(x - 5)
c) 10x(x - y) - 8(y - x)
= 10x(x - y) + 8(x - y)
= (x - y)(10x + 8)
= 2(x - y)(5x + 4)
d) (3x + 1)² - (x + 1)²
= (3x + 1 - x - 1)(3x + 1 + x + 1)
= 2x(4x + 2)
= 4x(2x + 1)
e) x³ + y³ + z³ - 3xyz
= x³ + y³ + 3x²y + 3xy² - 3xy(x + y) + z³ - 3xyz
= [(x + y)³ + z³] - [3xy(x + y) + 3xyz]
= (x + y + z)[(x + y)² - (x + y)z + z²] - 3xy(x + y + z)
= (x + y + z)(x² + 2xy + y² - xz - yz + z² - 3xy)
= (x + y + z)(x² + y² + z² - xy - xz - yz)
f) 5x² - 10xy + 5y² - 20z²)
= 5(x² - 2xy + y² - 4z²)
= 5[(x - y)² - (2z)²]
= 5(x - y - 2z)(x - y + 2z)
Dạng 3:
a: \(\dfrac{5xy-4y}{2x^2y^3}+\dfrac{3xy+4y}{2x^2y^3}\)
\(=\dfrac{5xy-4y+3xy+4y}{2x^2y^3}\)
\(=\dfrac{8xy}{2x^2y^3}=\dfrac{4}{xy^2}\)
b: \(\dfrac{x+3}{x-2}-\dfrac{4+x}{2-x}\)(ĐKXĐ: x<>2)
\(=\dfrac{x+3}{x-2}+\dfrac{x+4}{x-2}\)
\(=\dfrac{x+3+x+4}{x-2}=\dfrac{2x+7}{x-2}\)
c: \(\dfrac{x+1}{2x+6}+\dfrac{2x+3}{x^2+3x}\)(ĐKXĐ: \(x\notin\left\{0;-3\right\}\))
\(=\dfrac{x+1}{2\left(x+3\right)}+\dfrac{2x+3}{x\left(x+3\right)}\)
\(=\dfrac{x\left(x+1\right)+2\left(2x+3\right)}{2x\left(x+3\right)}\)
\(=\dfrac{x^2+x+4x+6}{2x\left(x+3\right)}\)
\(=\dfrac{x^2+5x+6}{2x\left(x+3\right)}=\dfrac{\left(x+3\right)\left(x+2\right)}{2x\left(x+3\right)}=\dfrac{x+2}{2x}\)
d: \(\dfrac{3}{x+3}\cdot\dfrac{x-6}{2}\)(ĐKXĐ: x<>-3)
\(=\dfrac{3\cdot\left(x-6\right)}{2\left(x+3\right)}\)
\(=\dfrac{3x-18}{2x+6}\)
e: \(\dfrac{2x+6}{3x^2-x}:\dfrac{x^2+3x}{1-3x}\)(ĐKXĐ: \(x\notin\left\{0;\dfrac{1}{3};-3\right\}\))
\(=\dfrac{2x+6}{3x^2-x}\cdot\dfrac{-3x+1}{x^2+3x}\)
\(=\dfrac{2\left(x+3\right)}{x\left(3x-1\right)}\cdot\dfrac{-\left(3x-1\right)}{x\left(x+3\right)}\)
\(=\dfrac{-2}{x^2}\)
f: Bạn chụp lại đề câu này nha, câu này mờ quá