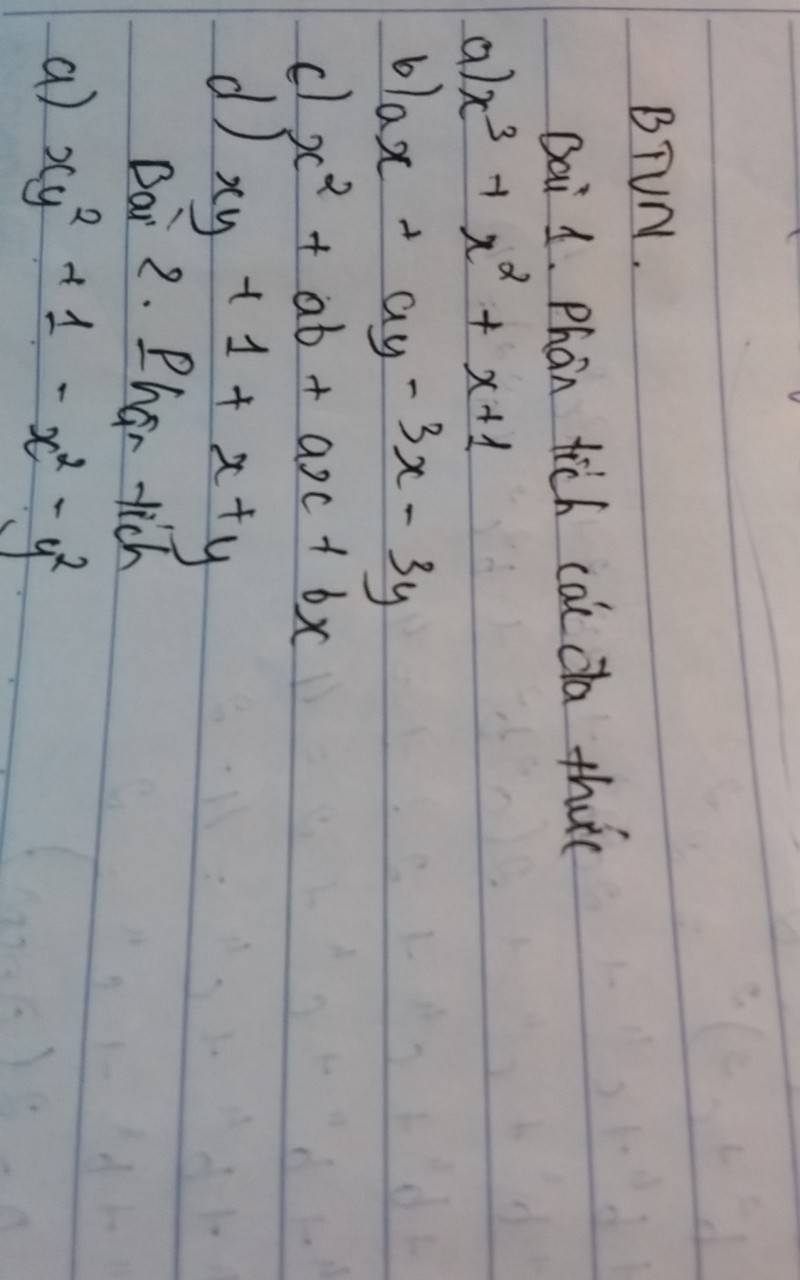Bài 3:
a: \(a\left(b^2+c^2\right)+b\left(c^2+a^2\right)+c\left(a^2+b^2\right)+2abc\)
\(=ab^2+ac^2+bc^2+ba^2+2abc+c\left(a^2+b^2\right)\)
\(=ab^2+ba^2+ac^2+bc^2+c\left(a^2+b^2+2ab\right)\)
\(=\left(ab^2+ba^2\right)+\left(ac^2+bc^2\right)+c\left(a+b\right)^2\)
\(=ab\left(a+b\right)+c^2\left(a+b\right)+c\left(a+b\right)^2\)
\(=\left(a+b\right)\left(ab+c^2+ac+bc\right)\)
\(=\left(a+b\right)\left[\left(ab+ac\right)+\left(c^2+bc\right)\right]\)
\(=\left(a+b\right)\left[a\left(b+c\right)+c\left(b+c\right)\right]\)
\(=\left(a+b\right)\left(b+c\right)\left(a+c\right)\)
b: \(a^3+b^3+c^3-3bac\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)\)
Bài 2:
a: \(xy^2+1-x^2-y^2\)
\(=\left(xy^2-y^2\right)-\left(x^2-1\right)\)
\(=y^2\left(x-1\right)-\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(y^2-x-1\right)\)
b: \(x^4-x^2+2x-1\)
\(=\left(x^4\right)-\left(x^2-2x+1\right)\)
\(=\left(x^2\right)^2-\left(x-1\right)^2\)
\(=\left(x^2-x+1\right)\left(x^2+x-1\right)\)
c: \(3a-3b+a^2-2ab+b^2\)
\(=\left(3a-3b\right)+\left(a^2-2ab+b^2\right)\)
\(=3\left(a-b\right)+\left(a-b\right)^2\)
\(=\left(a-b\right)\left(a-b+3\right)\)
b.
x4+x3-x2-x3-x2+x+x2+x+1
x2(x2+x-2)-x3-x2+x+x2+x-1
x2(x2+x-1)-x3-x2+x+1(x2+x-1)
từ dòng này mũ cho xuống dưới (viết mũ khó quá)
x2(x2+x-1)-(x3+x2-x)+1(x2+x-1)
x2(x2+x-1)-x(x2+x-1)+1(x2+x-2)
(x2-x+1)(x2+x-1)
c.