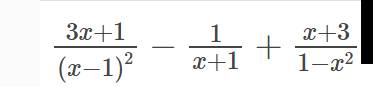ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(\dfrac{3x+1}{\left(x-1\right)^2}-\dfrac{1}{x+1}+\dfrac{x+3}{1-x^2}\)
\(=\dfrac{3x+1}{\left(x-1\right)^2}-\dfrac{1}{x+1}-\dfrac{x+3}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{\left(3x+1\right)\left(x+1\right)-\left(x-1\right)^2-\left(x+3\right)\left(x-1\right)}{\left(x-1\right)^2\cdot\left(x+1\right)}\)
\(=\dfrac{3x^2+4x+1-x^2+2x-1-\left(x^2+2x-3\right)}{\left(x-1\right)^2\cdot\left(x+1\right)}\)
\(=\dfrac{2x^2+6x-x^2-2x+3}{\left(x-1\right)^2\cdot\left(x+1\right)}\)
\(=\dfrac{x^2+4x+3}{\left(x-1\right)^2\cdot\left(x+1\right)}=\dfrac{\left(x+3\right)\left(x+1\right)}{\left(x-1\right)^2\cdot\left(x+1\right)}\)
\(=\dfrac{x+3}{\left(x-1\right)^2}\)