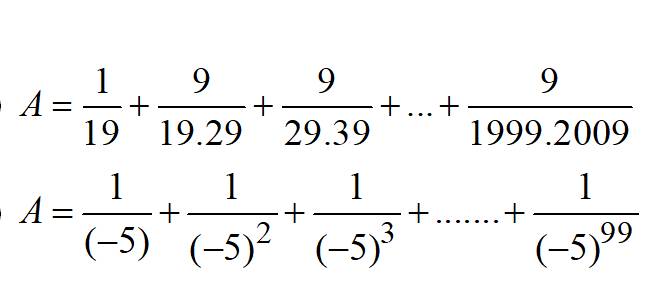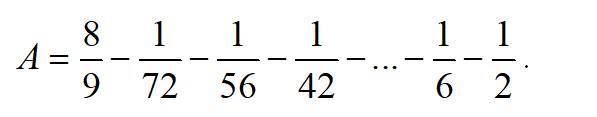a: \(A=\dfrac{1}{19}+\dfrac{9}{19\cdot29}+\dfrac{9}{29\cdot39}+...+\dfrac{9}{1999\cdot2009}\)
\(=\dfrac{1}{19}+\dfrac{9}{10}\left(\dfrac{10}{19\cdot29}+\dfrac{10}{29\cdot39}+...+\dfrac{10}{1999\cdot2009}\right)\)
\(=\dfrac{1}{19}+\dfrac{9}{10}\left(\dfrac{1}{19}-\dfrac{1}{29}+\dfrac{1}{29}-\dfrac{1}{39}+...+\dfrac{1}{1999}-\dfrac{1}{2009}\right)\)
\(=\dfrac{1}{19}+\dfrac{9}{10}\left(\dfrac{1}{19}-\dfrac{1}{2009}\right)\)
\(=\dfrac{1}{19}+\dfrac{9}{10}\cdot\dfrac{1990}{38171}\)
\(=\dfrac{1}{19}+\dfrac{1791}{38171}=\dfrac{200}{2009}\)
b: \(A=\left(-\dfrac{1}{5}\right)+\left(-\dfrac{1}{5}\right)^2+...+\left(-\dfrac{1}{5}\right)^{99}\)
=>\(\left(-\dfrac{1}{5}\right)\cdot A=\left(-\dfrac{1}{5}\right)^2+\left(-\dfrac{1}{5}\right)^3+...+\left(-\dfrac{1}{5}\right)^{100}\)
=>\(\left(-\dfrac{1}{5}\right)\cdot A-A=\left(-\dfrac{1}{5}\right)^2+\left(-\dfrac{1}{5}\right)^3+...+\left(-\dfrac{1}{5}\right)^{100}-\left(-\dfrac{1}{5}\right)-\left(-\dfrac{1}{5}\right)^2-...-\left(-\dfrac{1}{5}\right)^{99}\)
=>\(-\dfrac{6}{5}\cdot A=\left(-\dfrac{1}{5}\right)^{100}+\dfrac{1}{5}=\dfrac{1}{5^{100}}+\dfrac{1}{5}=\dfrac{1+5^{99}}{5^{100}}\)
=>\(A=\dfrac{-5^{99}-1}{5^{100}}:\dfrac{6}{5}=\dfrac{-5^{99}-1}{6\cdot5^{99}}\)
c: \(A=\dfrac{8}{9}-\dfrac{1}{2}-\dfrac{1}{6}-...-\dfrac{1}{72}\)
\(=\dfrac{8}{9}-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{8\cdot9}\right)\)
\(=\dfrac{8}{9}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}\right)\)
\(=\dfrac{8}{9}-1+\dfrac{1}{9}=0\)
\(A=\dfrac{1}{19}+\dfrac{9}{19.29}+\dfrac{9}{29.39}+...+\dfrac{9}{1999.2009}\)
\(A=\dfrac{1}{19}+\left(\dfrac{9}{19.29}+\dfrac{9}{29.39}+...+\dfrac{9}{1999.2009}\right)\)
\(A=\dfrac{1}{19}+\dfrac{9}{10}.\left(\dfrac{1}{19}-\dfrac{1}{29}+\dfrac{1}{29}-\dfrac{1}{39}+...+\dfrac{1}{1999}-\dfrac{1}{2009}\right)\)
\(A=\dfrac{1}{19}-\dfrac{9}{10}.\left(\dfrac{1}{19}-\dfrac{1}{2009}\right)\)
\(A=\dfrac{1}{19}-\dfrac{9}{10}.\dfrac{1990}{38171}\)
\(A=\dfrac{1}{19}-\dfrac{1791}{38171}\)
\(A=\dfrac{218}{38171}\)
_____________________
\(A=\dfrac{8}{9}-\dfrac{1}{72}-\dfrac{1}{56}-\dfrac{1}{42}-...-\dfrac{1}{6}-\dfrac{1}{2}\)
\(A=\dfrac{8}{9}-\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}\right)\)
\(A=\dfrac{8}{9}-\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}\right)\)
\(A=\dfrac{8}{9}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}\right)\)
\(A=\dfrac{8}{9}-\left(1-\dfrac{1}{9}\right)\)
\(A=\dfrac{8}{9}-\dfrac{8}{9}\)
\(A=0\)
\(#WendyDang\)