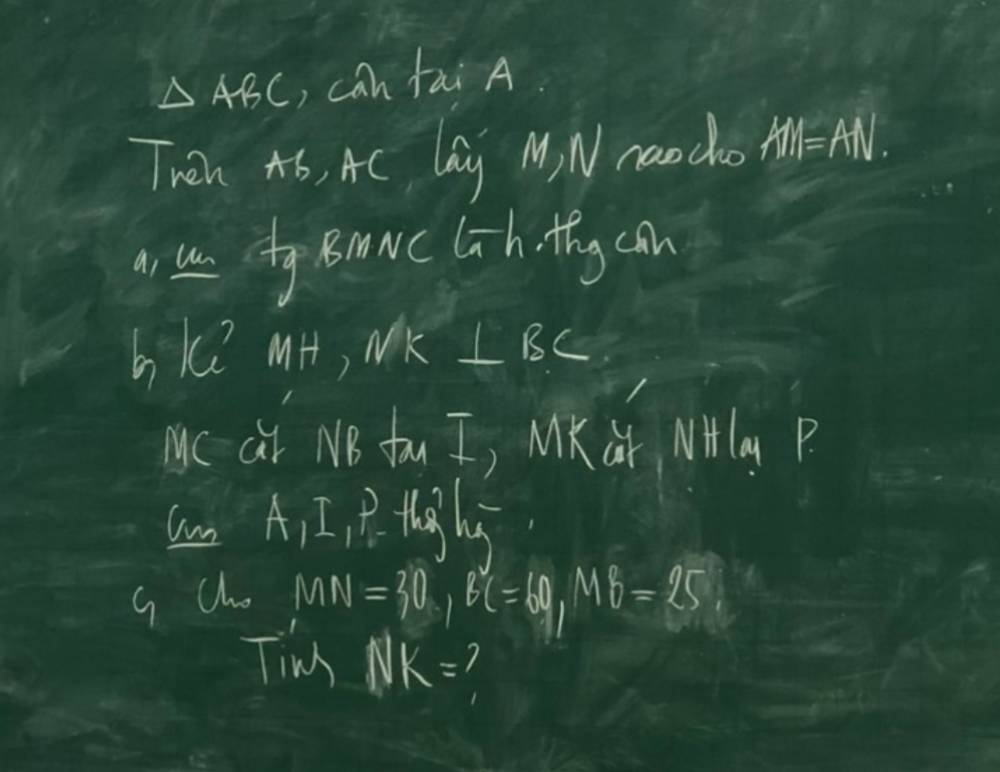a: Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
Xét tứ giác MNCB có MN//BC
nên MNCB là hình thang
Hình thang MNCB có \(\widehat{MBC}=\widehat{NCB}\)
nên MNCB là hình thang cân
b: Xét tứ giác MNKH có
MH//NK
MN//HK
Do đó: MNKH là hình bình hành
mà \(\widehat{MHK}=90^0\)
nên MNKH là hình chữ nhật
=>MK=NH và MK cắt NH tại trung điểm của mỗi đường
=>P là trung điểm chung của MK và NH và MK=NH
=>PK=PM=PH=PN
PH=PK
=>\(\widehat{PHK}=\widehat{PKH}\)
\(\widehat{PHK}+\widehat{PHB}=180^0\)
\(\widehat{PKH}+\widehat{PKC}=180^0\)
mà \(\widehat{PHK}=\widehat{PKH}\)
nên \(\widehat{PHB}=\widehat{PKC}\)
Xét ΔMHB vuông tại H và ΔNKC vuông tại N có
MB=NC
\(\widehat{MBH}=\widehat{NCK}\)
Do đó: ΔMHB=ΔNKC
=>BH=KC
Xét ΔPHB và ΔPKC có
PH=PK
\(\widehat{PHB}=\widehat{PKC}\)
HB=KC
Do đó: ΔPHB=ΔPKC
=>PB=PC
Xét ΔMBC và ΔNCB có
MB=NC
\(\widehat{MBC}=\widehat{NCB}\)
BC chung
Do đó: ΔMBC=ΔNCB
=>\(\widehat{MCB}=\widehat{NBC}\)
=>IB=IC
AB=AC
=>A nằm trên trung trực của BC(1)
IB=IC
=>I nằm trên trung trực của BC(2)
PB=PC
=>P nằm trên trung trực của BC(3)
Từ (1),(2),(3) suy ra A,I,P thẳng hàng