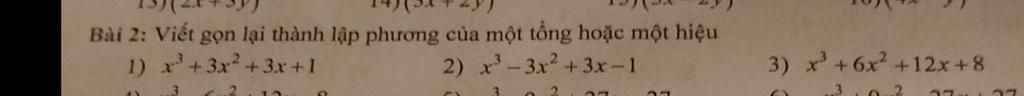Question

Answer 1

1) \(x^3+3x^2+3x+1\)

\(=x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3\)

\(=\left(x+1\right)^3\)

2) \(x^3-3x^2+3x-1\)

\(=x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3\)

\(=\left(x-1\right)^3\)

3) \(x^3+6x^2+12x+8\)

\(=x^3+3\cdot x^2\cdot2+3\cdot x\cdot2^2+2^3\)

\(=\left(x+2\right)^3\)

Answer 2

\(1)x^3+3x^2+3x+1\\=x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3\\=(x+1)^3\\2)x^3-3x^2+3x-1\\=x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3\\=(x-1)^3\\3)x^3+6x^2+12x+8\\=x^3+3\cdot x^2\cdot2+3\cdot x\cdot2^2+2^3\\=(x+2)^3\)

#\(Toru\)