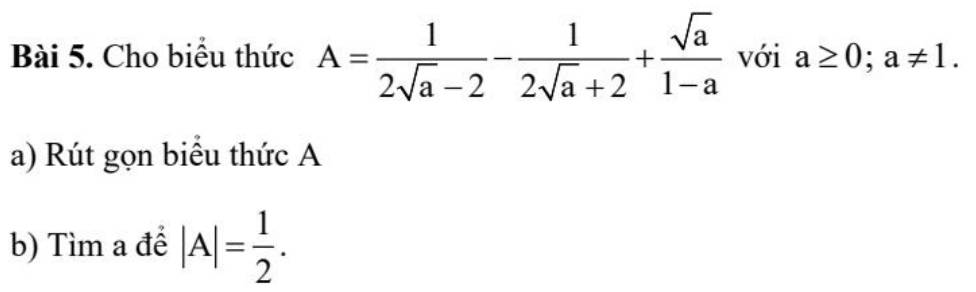a)
\(\dfrac{1}{2\sqrt{a}-2}-\dfrac{1}{2\sqrt{a}+2}+\dfrac{\sqrt{a}}{1-a}\left(a\ge0;a\ne1\right)\\ =\dfrac{1}{2\left(\sqrt{a}-1\right)}-\dfrac{1}{2\left(\sqrt{a}+1\right)}-\dfrac{\sqrt{a}}{a-1}\\ =\dfrac{\sqrt{a}+1}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}-\dfrac{\sqrt{a}-1}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}-\dfrac{2\sqrt{a}}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{\sqrt{a}+1-\sqrt{a}+1-2\sqrt{a}}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ =\dfrac{2-2\sqrt{a}}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ =\dfrac{-2\left(-1+\sqrt{a}\right)}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ =\dfrac{-1}{\sqrt{a}+1}\)
b)
\(\left|A\right|=\dfrac{1}{2}< =>\left[{}\begin{matrix}A=\dfrac{1}{2}\\A=-\dfrac{1}{2}\end{matrix}\right.\)
với `A=1/2` ta có
\(\dfrac{1}{2}=\dfrac{-1}{\sqrt{a}+1}\\ < =>\sqrt{a}+1=-2\\ < =>\sqrt{a}=-3\left(vl\right)\)
với `A=-1/2` ta có
\(-\dfrac{1}{2}=\dfrac{-1}{\sqrt{a}+1}\\ < =>-\sqrt{a}-1=-2\\ < =>\sqrt{a}=1\\ < =>a=1\left(ktm\right)\)
\(a,A=\dfrac{1}{2\sqrt{a}-2}-\dfrac{1}{2\sqrt{a}+2}+\dfrac{\sqrt{a}}{1-a}\) (ĐKXĐ: \(a\ge0;a\ne1\))
\(=\dfrac{\sqrt{a}+1}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}-\dfrac{\sqrt{a}-1}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}-\dfrac{\sqrt{a}}{a-1}\)
\(=\dfrac{\sqrt{a}+1-\left(\sqrt{a}-1\right)}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}-\dfrac{2\sqrt{a}}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{2-2\sqrt{a}}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{a}-1\right)}{2\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=-\dfrac{1}{\sqrt{a}+1}\)
Vậy \(A=-\dfrac{1}{\sqrt{a}+1}\)
\(b,\left|A\right|=\dfrac{1}{2}\Leftrightarrow\left|-\dfrac{1}{\sqrt{a}+1}\right|=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{1}{\sqrt{a}+1}=\dfrac{1}{2}\\-\dfrac{1}{\sqrt{a}+1}=-\dfrac{1}{2}\end{matrix}\right.\left(a\ge0\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-\sqrt{a}-1=2\\\sqrt{a}+1=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-\sqrt{a}=3\left(ktm\right)\\\sqrt{a}=1\end{matrix}\right.\)
\(\Leftrightarrow a=1\left(ktm\right)\)
Vậy không tìm được giá trị nào của \(x\) thoả mãn \(\left|A\right|=\dfrac{1}{2}\).
#\(Toru\)