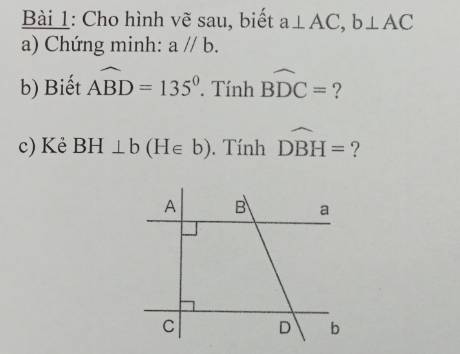
a) Ta có:
\(\left\{{}\begin{matrix}b\perp AC\\a\perp AC\end{matrix}\right.\)
\(\Rightarrow a//b\)
b) Ta có: a//b
\(\Rightarrow\widehat{ABD}+\widehat{BDC}=180^o\) (trong cùng phía)
\(\Rightarrow\widehat{BDC}=180^o-\widehat{ABD}\)
\(\Rightarrow\widehat{BDC}=180^o-135^o=45^o\)
c) Xét tam giác \(BHD\) ta có:
\(\widehat{BHD}+\widehat{BDH}+\widehat{DBH}=180^o\) (tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{DBH}=180^o+\widehat{BHD}-\widehat{BDH}\)
\(\Rightarrow\widehat{DBH}=180^o-45^o-90^o\)
\(\Rightarrow\widehat{DBH}=45^o\)
a)
Theo đề có: \(\left\{{}\begin{matrix}a\perp AC\\b\perp AC\end{matrix}\right.\Rightarrow a//b\) (theo tính chất 2 đường thẳng song song nhau)
b)
Vì a//b nên:
\(\widehat{ABD}=\widehat{BDb}=135^o\)
Theo kề bù:
\(\Rightarrow\widehat{BDC}=180^o-\widehat{BDb}=180^o-135^o=45^o\)
c)
Vì a//b nên: \(\widehat{aBb}=\widehat{BDC}=45^o\)
Vì BH⊥b
=> BH⊥a (vì a//b)
=> \(\widehat{ABH}=90^o\)
Theo kề bù:
\(\widehat{ABH}+\widehat{DBH}+\widehat{aBb}=180^o\\ \Rightarrow\widehat{DBH}=180^o-90^o-45^o=45^o\)
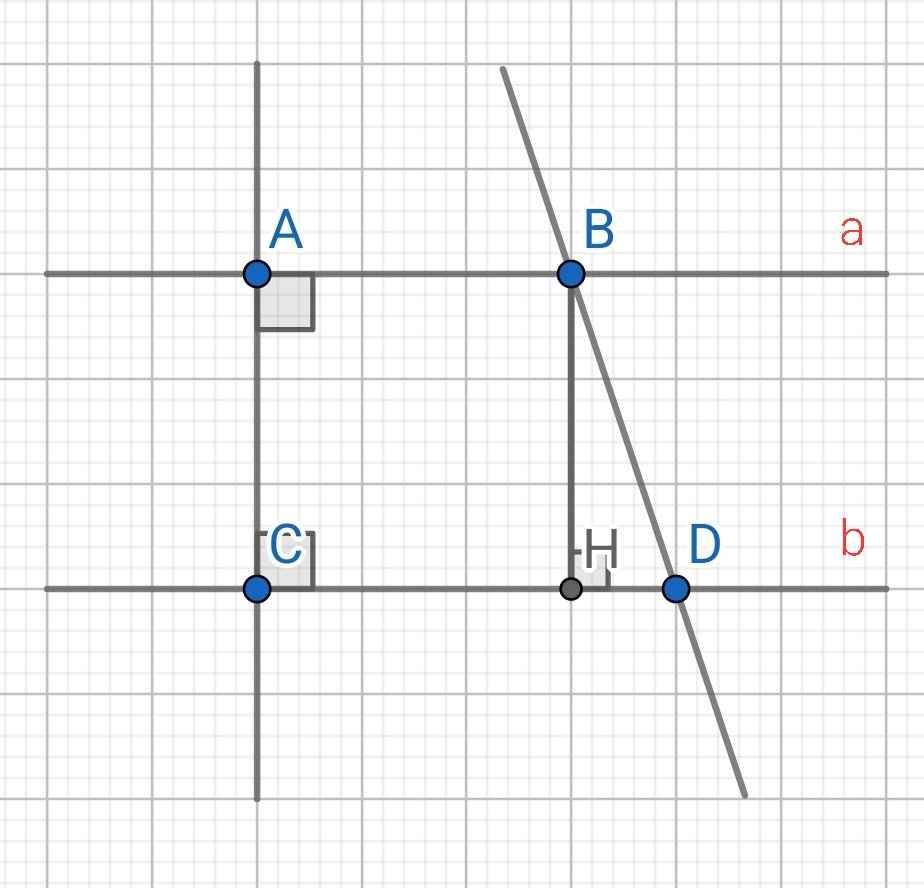
a) Do a ⊥ AC (gt)
b ⊥ AC (gt)
⇒ a // b
b) Do a // b (cmt)
⇒ ∠BDb = ∠ABD = 135⁰ (so le trong)
Ta có:
∠BDb + ∠BDC = 180⁰ (kề bù)
⇒ ∠BDC = 180⁰ - ∠BDb
= 180⁰ - 135⁰
= 45⁰
c) Do BH ⊥ b (gt)
AC ⊥ b (gt)
⇒ BH // AC
⇒ ∠ABH = ∠BHD = 90⁰ (so le trong)
⇒ ∠DBH = ∠ABD - ∠ABH
= 135⁰ - 90⁰
= 45⁰