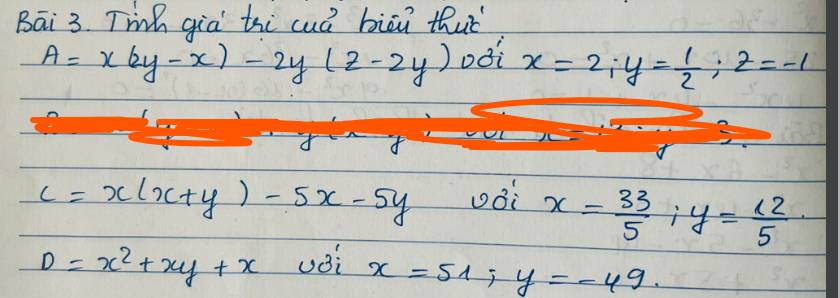`c, C=x(x+y)-5x-5y`
`=x(x+y)-(5x+5y)`
`=x(x+y)-5(x+y)`
`=(x+y)(x-5)`
Với `x=33/5` và `y=12/5`
Ta có : `(x+y)(x-5)`
`=(33/5+12/5)(33/5-5)`
`=45/5 * 8/5`
`=72/5`
__
`x^2+xy+x`
`=x(x+y+1)`
Với `x=51` và `y=-49`
Ta có : `x(x+y+1)`
`=51(51-49+1)`
`=51*3`
`= 153`
`@ yl`
`x(2y-x)-2y(z-2y)`
Tại `x=2;y=1/2` và `z=-1`
`=2(2*1/2 -2)-2*1/2(-1-2*1/2)`
`=2(1-2)-1(-1-1)`
`=2*(-1)-1*(-2)`
`= -2+2`
`=0`
\(a,A=x\left(zy-x\right)-2y\left(z-2y\right)\)
Thay \(x=2\), \(y=\dfrac{1}{2}\) và \(z=-1\) vào A, ta được:
\(A=2\left(-\dfrac{1}{2}-2\right)-2.\dfrac{1}{2}\left(-1-2.\dfrac{1}{2}\right)\)
\(=2.\dfrac{-5}{2}-\left(-2\right)\)
\(=-5+2=-3\)
\(c,C=x\left(x+y\right)-5x-5y\)
\(=x\left(x+y\right)-5\left(x+y\right)\)
\(=\left(x+y\right)\left(x-5\right)\)
Thay \(x=\dfrac{33}{5};y=\dfrac{12}{5}\) vào C, ta được:
\(C=\left(\dfrac{33}{5}+\dfrac{12}{5}\right)\left(\dfrac{33}{5}-5\right)\)
\(=\dfrac{45}{5}.\dfrac{8}{5}\)
\(=\dfrac{9.8}{5}=\dfrac{72}{5}\)
\(d,D=x^2+xy+x\)
\(=x\left(x+y+1\right)\)
Thay \(x=51;y=-49\) vào D, ta được:
\(D=51.\left(51-49+1\right)\)
\(=51.\left(2+1\right)\)
\(=51.3=153\)