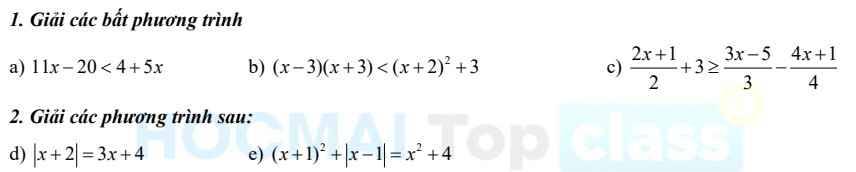Question

Answer 1

a) \(11x-20< 4+5x\)

\(\Leftrightarrow11x-5x< 4+20\)

\(\Leftrightarrow6x< 24\)

\(\Leftrightarrow x< 4\)

b) \(\left(x-3\right)\left(x+3\right)< \left(x+2\right)^2+3\)

\(\Leftrightarrow x^2-9< x^2+4x+4+3\)

\(\Leftrightarrow x^2-9< x^2+4x+7\)

\(\Leftrightarrow x^2-x^2-4x< 7+9\)

\(\Leftrightarrow-4x< 16\)

\(\Leftrightarrow x< -4\)

c) \(\dfrac{2x+1}{2}+3\ge\dfrac{3x-5}{3}-\dfrac{4x+1}{4}\)

\(\Leftrightarrow\dfrac{6\left(2x+1\right)}{12}+\dfrac{36}{12}\ge\dfrac{4\left(3x-5\right)}{12}-\dfrac{3\left(4x+1\right)}{12}\)

\(\Leftrightarrow12x+6+36\ge12x-20-12x-3\)

\(\Leftrightarrow12x+42\ge-23\)

\(\Leftrightarrow12x\ge-23-42\)

\(\Leftrightarrow12x\ge-65\)

\(\Leftrightarrow x\ge-\dfrac{65}{12}\)

Answer 2

  

Answer 3

bài 2
d) TH1: x+2>0  =>  x>-2
<=> x+2=3x+4
<=> x=-1(t/m)
TH2: x+2<0  =>  x<-2
<=> -x-2=3x+4
<=> x=-3/2(loại)
 

Answer 4

  cái này mình sửa lại câu c chút xíu nha

Answer 5

e) TH1: x-1>0  => x>1
<=> (x+1)^2 + x-1= x^2 +4
<=> x^2 +2x +1 +x-1=x^2 +4
<=>x=4/3(t/m)
TH2: x-1<0  => x<1
<=> (x+1)^2 -x+1= x^2 +4
<=> x^2 +2x+1-x+1=x^2 +4
<=> x=2(loại)

Answer 6

a) <=> 11x-5x<4+20
<=> x<4
b) <=> x^2 -9<x^2 +4x+4+3
<=> x^2-x^2-4x<4+3+9
<=> x>-4
c) \(\Leftrightarrow\dfrac{6\left(2x+1\right)}{12}+\dfrac{36}{12}\ge\dfrac{4\left(3x-5\right)}{12}-\dfrac{3\left(4x+1\right)}{12}\)
<=> 12x+6+36\(\ge\)12x-20-12x-3
<=> 12x-12x+12x\(\ge\)-20-3-6-36
<=> x\(\ge\)\(-\dfrac{65}{12}\)