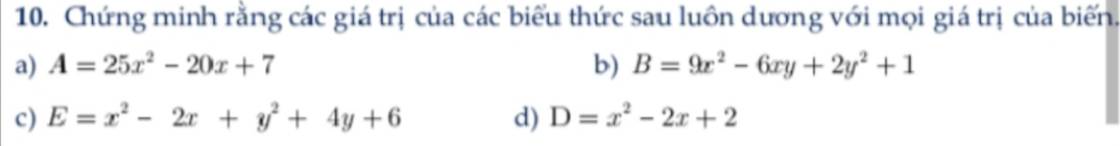a: A=25x^2-20x+4+3
=(5x)^2-2*5x*2+2^2+3
=(5x-2)^2+3>=3>0 với mọi x
=>A luôn dương với mọi x
b: B=9x^2-6xy+y^2+y^2+1
=(3x-y)^2+y^2+1>=1>0 với mọi x,y
=>B luôn dương
c: E=x^2-2x+1+y^2+4y+4+1
=(x-1)^2+(y+2)^2+1>=1 với mọi x,y
=>E luôn dương
d: D=x^2-2x+2
=x^2-2x+1+1
=(x-1)^2+1>=1>0 với mọi x
=>D luôn dương
\(A=25x^2-20x+7\\ =\left(5x\right)^2-2.5x.2+2^2+3\\ =\left(5x+2\right)^2+3\ge3\forall x\in R\left(Vì:\left(5x+2\right)^2\ge0\forall x\in R\right)\)
Vậy: GT biểu thức luôn dương với mọi giá trị của biến
\(B=9x^2-6xy+2y^2+1\\ =\left(3x\right)^2-2.3x.y+y^2+y^2+1\\ =\left(3x-y\right)^2+y^2+1\\ Ta.có:\left(3x-y\right)^2\ge0\forall x,y\in R\\ Tiếp,đến:y^2\ge0\forall y\in R\\ Vậy:\left(3x-y\right)^2+y^2+1\ge1\forall x,y\in R\)
Vậy: GT biểu thức luôn dương với mọi giá trị của biến