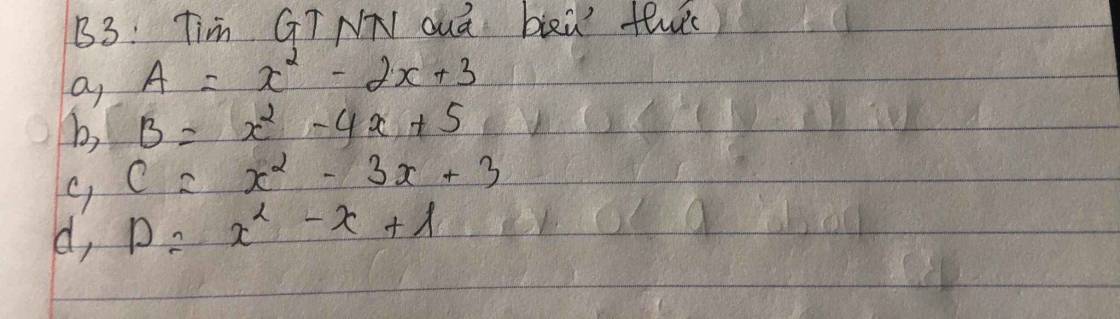\(a,A=x^2-2x+3\)
\(=x^2-2.x.1+1+2\)
\(=x^2-2.x.1+1^2+2\)
\(=\left(x-1\right)^2+2\)
Vì \(\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-1\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra khi:
\(\left(x-1\right)^2+2=2\)
\(\Rightarrow\left(x-1\right)^2=0\)
\(\Rightarrow x-1=0\)
\(\Rightarrow x=1\)
Vậy GTNN của A = 2 tại \(x=1\)
\(b,B=x^2-4x+5\)
\(=x^2-2.x.2+2^2+1\)
\(=\left(x-2\right)^2+1\)
Vì \(\left(x-2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-2\right)^2+1\ge1\forall x\)
Dấu "=" xảy ra khi:
\(\left(x-2\right)^2+1=1\)
\(\Rightarrow\left(x-2\right)^2=0\)
\(\Rightarrow x-2=0\)
\(\Rightarrow x=2\)
Vậy giá trị nhỏ nhất của B = 1 tại x = 2
\(c,C=x^2-3x+3\)
\(=x^2-2.x.\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+\dfrac{3}{4}\)
\(=\left(x-\dfrac{3}{2}\right)^2\)\(+\dfrac{3}{4}\)
Vì \(\left(x-\dfrac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu "=" xảy ra khi:
\(\left(x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}=\dfrac{3}{4}\)
\(\Rightarrow\left(x-\dfrac{3}{2}\right)^2=0\)
\(\Rightarrow x-\dfrac{3}{2}=0\)
\(\Rightarrow x=\dfrac{3}{2}\)
Vậy GTNN của C = \(\dfrac{3}{4}\) tại \(x=\dfrac{3}{2}\)
\(d,D=x^2-x+1\)
\(=x^2-2.x.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Vì \(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu "=" xảy ra khi:
\(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\dfrac{3}{4}\)
\(\Rightarrow\left(x-\dfrac{1}{2}\right)^2=0\)
\(\Rightarrow x-\dfrac{1}{2}=0\)
\(\Rightarrow x=\dfrac{1}{2}\)
Vậy GTNN của D = \(\dfrac{3}{4}\) tại \(x=\dfrac{1}{2}\)
*Hàng đẳng thức số 2: \(\left(a-b\right)^2=a^2-2.a.b+b^2\)
a: =x^2-2x+1+2=(x-1)^2+2>=2
Dấu = xảy ra khi x=1
b: =x^2-4x+4+1=(x-2)^2+1>=1
Dấu = xảy ra khi x=2
d: =x^2-x+1/4+3/4=(x-1/2)^2+3/4>=3/4
Dấu = xảy ra khi x=1/2
c: =x^2-3x+9/4+3/4
=(x-3/2)^2+3/4>=3/4
Dấu = xảy ra khi x=3/2