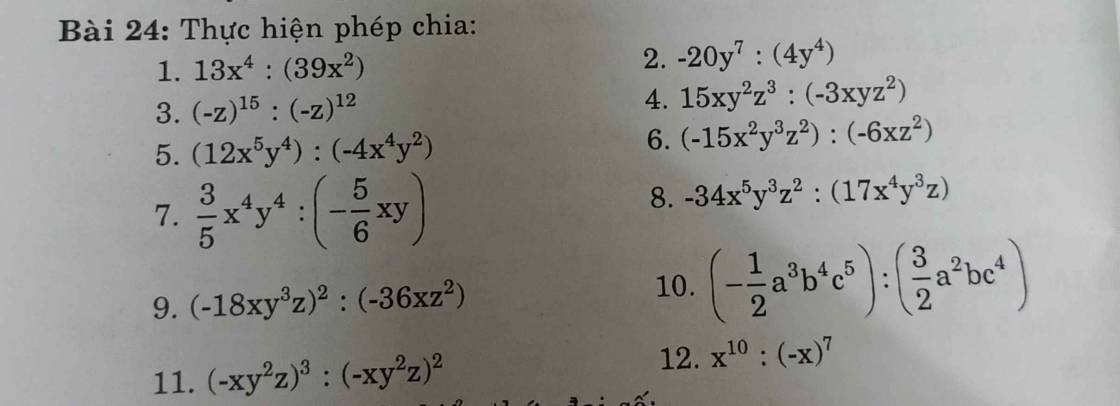1: \(=\dfrac{13}{39}\cdot\dfrac{x^4}{x^2}=\dfrac{1}{3}x^2\)
2: \(=\dfrac{-20}{4}\cdot\dfrac{y^7}{y^4}=-5y^3\)
3: =(-z)^15-12=(-z)^3=-z^3
4: \(=\dfrac{-15}{3}\cdot\dfrac{x}{x}\cdot\dfrac{y^2}{y}\cdot\dfrac{z^3}{z^2}=-5yz\)
5: \(=\dfrac{-12}{4}\cdot\dfrac{x^5}{x^4}\cdot\dfrac{y^4}{y^2}=-3xy^2\)
6: \(=\dfrac{15}{6}\cdot\dfrac{x^2y^3z^2}{xz^2}=\dfrac{5}{2}xy^3\)
7: =(-3/5:5/6)*x^4y^4:xy
=-18/25x^3y^3
8: =-34/17*x^5y^3z^2:x^4y^3z
=-2xz
12: =(-x)^10:(-x)^7=(-x)^3=-x^3
11: =(-xy^2z)^3-2=(-xy^2z)^1=-xy^2z
`@` `\text {Ans}`
`\downarrow`
`1,`
\(13x^4\div39x^2\)
`= (13 \div 39)*(x^4 \div x^2)`
`= 1/3x^2`
`3,`
\(\left(-z\right)^{15}\div\left(-z\right)^{12}\)
`=`\(\left(-z\right)^{15-12}=\left(-z\right)^3\)
`2,`
\(-20y^7\div4y^4\)
`=(-20 \div 4)*(y^7 \div y^4)`
`= -5y^3`
`4,`
\(15xy^2z^3\div\left(-3xyz^2\right)\)
`= [15 \div (-3)]*(x \div x)*(y^2 \div y)*(z^3 \div z^2)`
`= -5yz`
`5,`
\(12x^5y^4\div\left(-4x^4y^2\right)\)
`= [ 12 \div (-4)]*(x^5 \div x^4)*(y^4 \div y^2)`
`= -3xy^2`
`6,`
\(\left(-15xy^3z^2\right)\div\left(-6xz^2\right)\)
`= (-15 \div -6) * (x \div x) * y^3 * (z^2 \div z^2)`
`= 5/2y^3`
`7,`
\(\dfrac{3}{5}x^4y^4\div\left(-\dfrac{5}{6}xy\right)\)
`= [ 3/5 \div (-5/6)]*(x^4 \div x)*(y^4 \div y)`
`= -18/25x^3y^3`
`8,`
\(-34x^5y^3z^2\div17x^4y^3z\)
`= (-34 \div 17)*(x^5 \div x^4)*(y^3 \div y^3)*(z^2 \div z)`
`= -2xz`
`9,`
\(\left(-18xy^3z\right)^2\div\left(-36xz^2\right)\)
`= 324x^2y^6z^2 \div (-36xz^2)`
`= [ 324 \div (-36)] * (x^2 \div x)*y^6 *(z^2 \div z^2)`
`= -9xy^6`
`10,`
\(\left(-\dfrac{1}{2}a^3b^4c^5\right)\div\left(\dfrac{3}{2}a^2bc^4\right)\)
`= (-1/2 \div 3/2)*(a^3 \div a^2)*(b^4 \div b)*(c^5 \div c^4)`
`= -1/3ab^3c`
`11,`
\(\left(-xy^2z\right)^3\div\left(-xy^2z\right)^2\)
`= -x^3y^6z^3 \div (-x^2y^4z^2)`
`= y^2`
`12,`
\(x^{10}\div\left(-x\right)^7\)
`= (-x)`\(^{10-7}\)
`= (-x)^3`
`@` `\text {Kaizuu lv u.}`