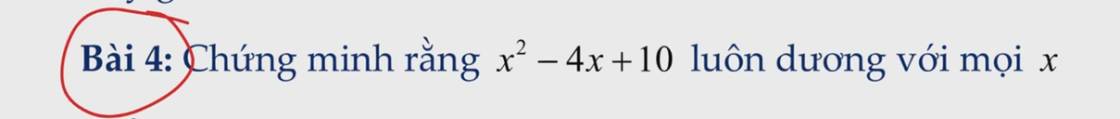Question

Answer 1

\(x^2-4x+10=x^2-4x+4+6=\left(x-2\right)^2+6\)

Ta có: \(\left\{{}\begin{matrix}\left(x-2\right)^2\ge0\\6>0\end{matrix}\right.\Rightarrow\left(x-2\right)^2+6\) luôn dương với mọi x

Answer 2

\(x^2-4x+10\\ \Leftrightarrow x^2-4x+4+6\\ \Leftrightarrow\left(x-2\right)^2+6\)

⇒ \(\left(x-2\right)^2\) dương (luôn đúng)

Vậy \(x^2-4x+10\) luôn dương với mọi \(x\)