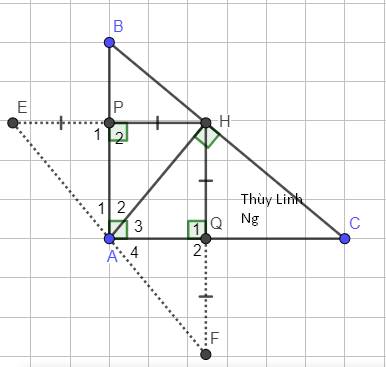
1: Xet ΔAPE vuông tại P và ΔAPH vuông tại P có
AP chung
PE=PH
=>ΔAPE=ΔAPH
Xet ΔAQH vuông tại Q và ΔAQF vuông tại Q có
AQ chung
QH=QF
=>ΔAQH=ΔAQF
2: góc EAF=góc EAH+góc FAH
=2(góc BAH+góc CAH)
=180 độ
=>E,A,F thẳng hàng
mà AE=AF
nên A là trung điểm của EF
`1)`
+, Có `HP⊥AB=>hat(P_1)=hat(P_2)(=90^0)`
Xét `Delta APE` và `Delta APH` có :
`{:(AP-chung),(hat(P_1)=hat(P_2)(=90^0)),(EP=HP(GT)):}}`
`=>Delta APE=Delta APH(c.g.c)(đpcm)`
+, Có `HQ⊥AC=>hat(Q_1)=hat(Q_2)(=90^0)`
Xét `Delta AQH` và `Delta AQF` có :
`{:(AQ-chung),(hat(Q_1)=hat(Q_2)(=90^0)),(HQ=FQ(GT)):}}`
`=>Delta AQH=Delta AQF(c.g.c)(đpcm)`
`2)`
Có `Delta APE=Delta APH(cmt)=>hat(A_1)=hat(A_2)(1)`
`Delta AQH=Delta AQF(cmt)=>hat(A_3)=hat(A_4)(3)`
Xét `hat(EAF)` có :
`hat(EAF)=hat(EAH)+hat(FAH)`
mà +,`hat(EAH)=hat(A_1)+hat(A_2) (2)`
Từ `(1)` và `(2)=>hat(EAH)=2hat(A_1)`
+, `hat(FAH)=hat(A_3)+hat(A_4)(4)`
Từ `(3)` và `(4)=>hat(FAH)=2hat(A_3)`
Nên `hat(EAF)=2hat(A_1)+2hat(A_3)=2*(hat(A_1)+hat(A_3))`
mà `hat(A_1)+hat(A_3)=90^0(=hat(BAC))`
nên `hat(EAF)=2*90^0=180^0`
`=>E;A;F` thẳng hàng